1. Introduction
2. Materials and Methods
2.1 Materials
2.2 Drying methods
2.3 Moisture content and drying rate calculation
2.4 Effective moisture diffusivity calculation
2.5 Energy consumption calculation
2.6 ANN modeling method
3. Results and Discussion
3.1 MPP drying curves
3.2 Effective moisture diffusivity
3.3 Energy consumption
3.4 ANN modeling of drying kinetics
4. Conclusions
1. Introduction
The molded pulp product (MPP) is a three-dimensional paper-based material that is usually made from plant fibers or recycled fibers. It has been used widely in the packaging sector as a green and environmentally friendly packaging material, including food, beverage, and electric devices, etc.1) The demand for MPP will increase dramatically in the future to achieve the climate neutrality target.
Generally, MPP is manufactured by pulp preparation, forming, pressing, drying, and post-processing.2) The MPP drying is an energy-intensive process, in which the tensile strength, the puncture resistance, and the stiffness are determined meanwhile.3) The cost of energy required for drying MPP is about 8 to 20 times higher than that needed for preforming.4) Therefore, it represents the most energy- using section in the entire MPP manufacturing process. Research and development of MPP drying technologies can not only reduce energy consumption but also improve the product quality.
In-mold drying and demolding drying are two common drying methods for MPP. In-mold drying refers to a drying method that directly heats inside the hot press mold. This method requires a significant investment, but the resulting product has even moisture distribution, precise dimensions, and an attractive appearance, making it suitable for more sophisticated products.5) Demolding drying, in contrast, is a process in which wet products are dried in a tunnel-type dryer after extrusion molding. It is characterized by ease of automation and large-scale production, mainly including convective drying, far-infrared drying, and microwave drying.6) Among them, convective drying is currently the most widely used method for MPP. However, the application of microwave has shown promising in intensifying the drying process.7) Compared with convective drying, it has the advantages of a rapid heating rate, short drying time, and low energy consumption. Demiray et al.8) found that the microwave drying enhanced the drying rate of onion slices as a result of increasing the effective moisture diffusivity as compared to the convective drying. Behera and Balasubramanian9)compared the efficiency of thin layer drying of microalgae through convective drying and microwave drying showing the later process to be much faster and efficient with higher effective diffusivity and lower specific energy requirements. Guemouni et al.10) studied the drying characteristics of tomato slices under convective and microwave drying, and concluded that the microwave drying could shorten the drying time by 96% while using 97% lower energy consumption at the power level of 900 W.
In the drying process, the prediction of moisture content is crucial for improving the overall performance. Although mathematical modeling can achieve good regression of experimental data under specific drying conditions, it cannot provide a universal equation that describes the drying process of every product. In contrast, artificial neural networks (ANN) have several advantages, such as the strong learning ability and applicability to nonlinear processes. Therefore, using ANN can predict moisture changes well during the drying process. It has been successfully used to simulate the drying process.11) Taheri et al.12) used microwave power, fluidized air temperature, and drying time as input parameters to establish the ANN model to predict the temperature and moisture content of lentil seeds in a microwave-fluidized bed dryer. Sun and Ling13) used temperature and time as input parameters to establish a genetic algorithm-back propagation model to predict the moisture content of wheat during hot air drying. Beigi and Torki14) used ANN to simulate the microwave drying of onion slices, with microwave power, sample thickness, and drying time as the input parameters.
This paper investigated the microwave drying characteristics of MPP at 500 W and compared it with the convective drying method. The drying kinetics, the effective moisture diffusivity, and the energy consumption were evaluated for the two drying methods. Furthermore, an ANN modeling was used to predict the drying kinetics of MPP.
2. Materials and Methods
2.1 Materials
The raw material used in this study was the wet MPP sample. It was made upon of bamboo pulp and sugarcane pulp, with the ratio of 65% and 35%. The chemicals include bleaching agents, adhesives, and waterproof agents, among others. The original size of which was 200 mm×100 mm×2.4 mm. The initial mass of the wet sample was 54.0 ± 0.5 g and the initial moisture content was 1.68 ± 0.05 g water/g fiber.
2.2 Drying methods
2.2.1 Convective drying method
The convective drying experiment was conducted at a temperature of 105℃. When the temperature of the hot air reached the set conditions and remained stable, the wet sample was placed in the drying oven (IMT-9030A, Dongguan International Material Tester Co, Ltd, China). The wet sample weight was measured at intervals of 2-minute using an electronic balance with an accuracy of 0.01 g until the moisture content of the sample reached 0.10 ± 0.01 g water/g fiber. The electronic balance was placed at the temperature of 25℃ and 55% relative humidity. To ensure the accuracy of the experiment, the entire weighing process was completed within 5 seconds to minimize errors. The experiment was repeated three times to ensure the accuracy and consistency of the results.
2.2.2 Microwave drying method
For microwave drying, the wet sample was placed in the microwave vacuum drying oven (RWBZ-08S, Nanjing Suenrui Drying Equipment Co., LTD, China). The experiment was carried out three times at 500 W microwave power at 2450 MHz. The same method for measuring the sample weight was used in the microwave drying experiments.
2.3 Moisture content and drying rate calculation
The dry basis moisture content (M, g water/g fiber) and drying rate (DR, g water/(g fiber·min)) of MPP are calculated according to Eq. 1 and Eq. 2.
where mi and md are the initial mass and absolute dried mass of the product (g), t1 and t2 are the drying time (min), Mt1 and Mt2 are the moisture content of MPP at time t1 and t2 (g water/g fiber).
The drying curve of MPP during the drying process adopts the curve of moisture ratio changing with time. The moisture ratio (MR) of MPP is calculated according to Eq. 3.
where Mt is the moisture content at time t (g water/g fiber), Mi is the initial moisture content (g water/g fiber) and Me is the equilibrium moisture content (g water/g fiber).
2.4 Effective moisture diffusivity calculation
In the MPP drying process, the moisture transport characteristics can be characterized by the effective moisture diffusivity (Deff). It is affected by pulp properties, moisture content, drying temperature, wind velocity, and microwave power. Assuming that internal water transfer is the main mechanism, according to Fick's second diffusion law, the change of moisture content with drying time can be expressed as Eq. 4.
When the MPP is assumed to be one-dimensional with uniform initial moisture content, the solution of Eq. 5 could be obtained.15)
where n is the positive integer, L is the half-thickness of MPP (m), and t is the drying time (s).
For a long drying time of MPP, the solution of Fick’s equation can be simplified with the first term of Eq. 5. and can be rewritten as Eq. 6 in a logarithmic form.
Thus, the value of Deff (m2/s) could be obtained from the slope keff of the curve between ln (MR) and t.
2.5 Energy consumption calculation
The energy consumption of convective drying for the MPP is calculated using Eq. 7.
where Qc is the energy consumption of convective drying (J), m is the air flux (kg/s), cp is the specific heat of air (J/(kg·℃)), ΔT is the temperature difference for heating the air (℃), and t is drying time (s).
The energy consumption of microwave drying for the MPP is calculated using Eq. 8.
where Qm is the energy consumption of microwave drying (J), P is the microwave power (W), and t is the drying time of microwave (s).
2.6 ANN modeling method
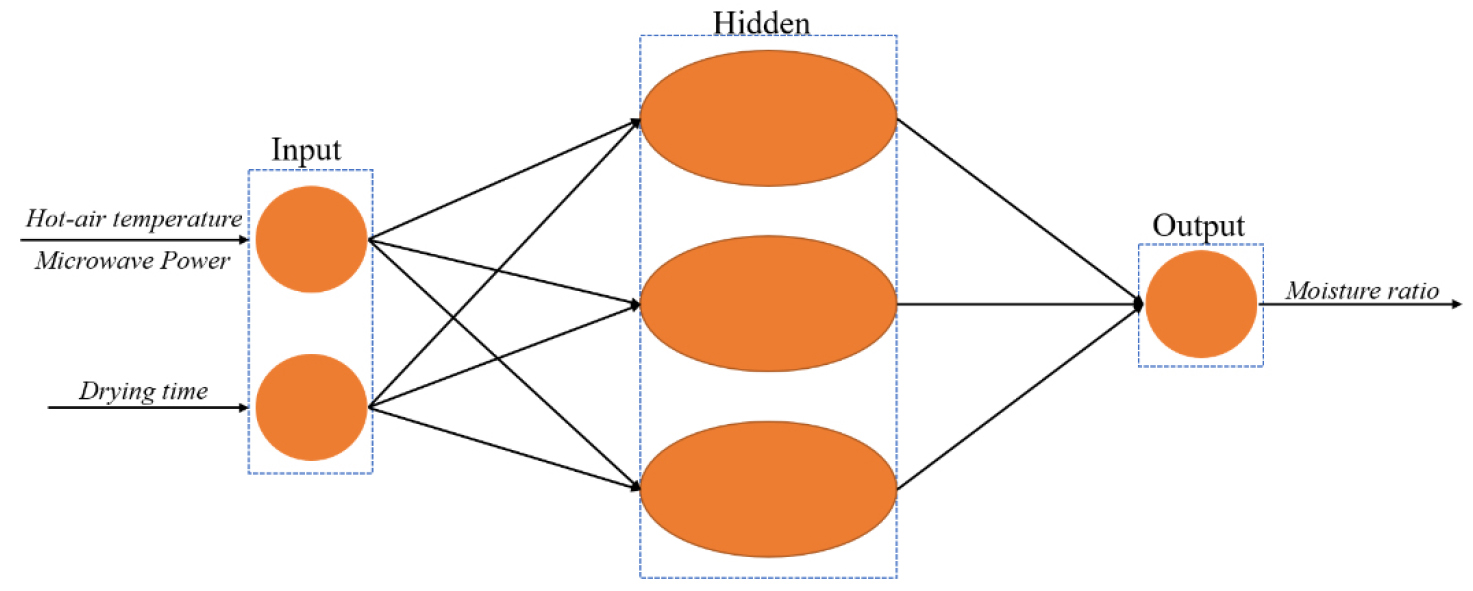
An ANN model was established and tested using MATLAB. The multi-layer feedforward network was selected, consisting of an input layer, a hidden layer, and an output layer, as presented in Fig. 1. Levenberg-Marquardt training algorithm was used to train the network. Based on the experimental results and research parameters, in the convective drying model, the input variables of the hot-air temperature (T) and drying time (t) were used for the input layer, and moisture ratio was chosen for the output layer. In the microwave drying model, the input variables were microwave power (P) and drying time (t). The experimental data was mixed and then divided into training, validation, and testing subsets. 70% of the dataset was used to calculate the gradient and train the network weights and biases. 15% was utilized for confirmation (to prevent overfitting), and the remaining was used as the testing set.
To obtain the best neural network model, a trial-and-error method was employed to determine the network parameters, including transfer function, training algorithm, number of hidden layers, and number of neurons in each hidden layer. The model performance was evaluated using the coefficient of determination (R2) and root mean square error (RMSE).16)
3. Results and Discussion
3.1 MPP drying curves
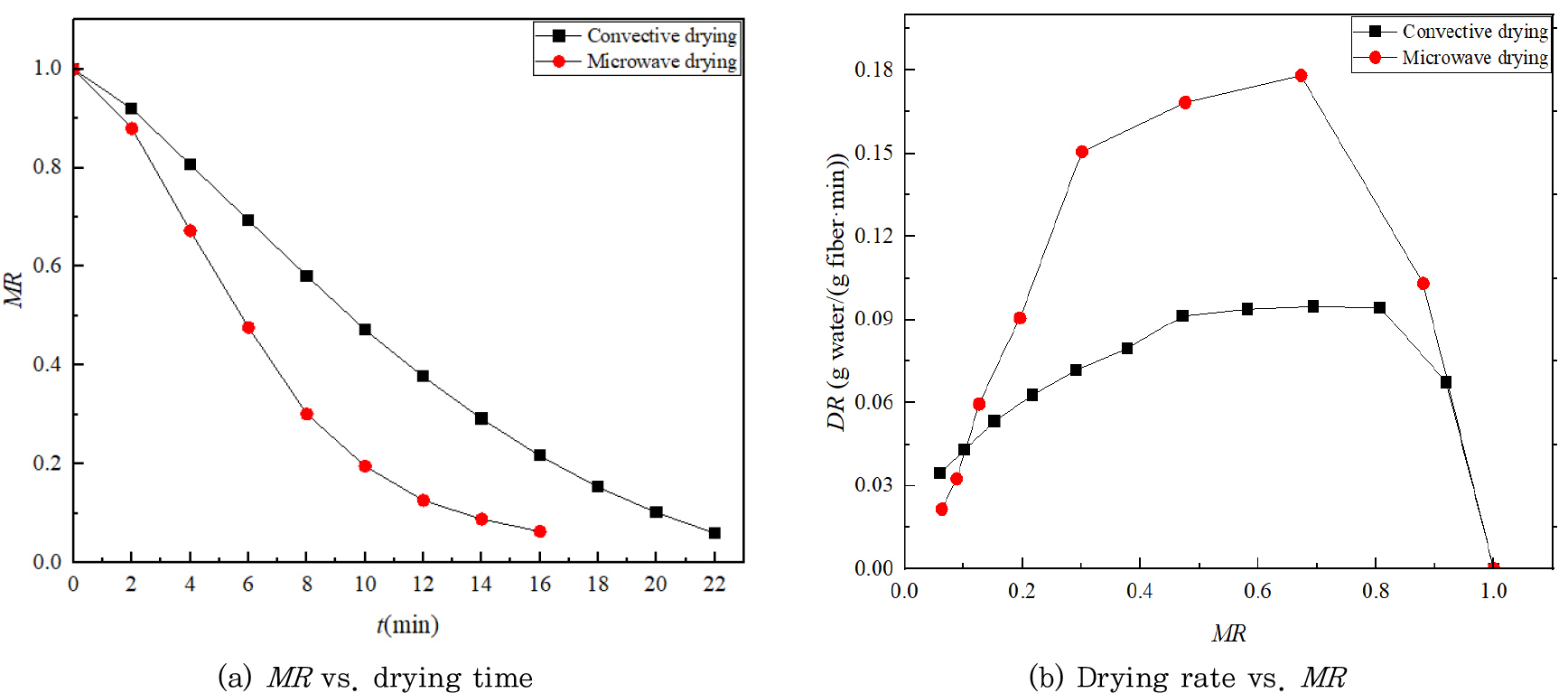
Fig. 2 shows the drying curves of MPP during the convective and microwave drying process. As shown in Fig. 2(a), the convective drying time was 22 min. From 0 to 4 min, the moisture ratio decreased from the initial value of 1 to 0.8, with a relatively fast rate of change. From 4 to 10 min, the moisture ratio decreased from 0.8 to 0.47, and the rate of change in moisture ratio remained almost constant. From 10 to 22 min, the moisture ratio decreased to 0.05, with a slower rate of change. The three periods were better reflected in Fig. 2(b). In the convective drying, the drying rate gradually increased when the moisture ratio was between 0.8 and 1, and the drying process was in the warm-up rate period. Then when the moisture ratio was between 0.47 and 0.8, the drying process was in the constant rate period, and the drying process was in the falling rate period when the moisture ratio was below 0.47.
As shown in Fig. 2(a), for the microwave drying, it only took 16 min. The drying time was shortened by 27% compared to the convective drying. From 0 to 4 min, the moisture ratio decreased from the initial value of 1 to 0.67, with a relatively fast rate of change. From 4 to 16 min, the moisture ratio decreased to 0.06, with a slower rate of change. This was also shown in Fig. 2(b). The drying rate gradually increased when the moisture ratio was between 0.67 and 1, and the drying process was in the warm-up rate period. When the moisture ratio reached 0.67, the MPP drying rate began to reduce dramatically in the falling rate period. The constant rate drying period did not exist for the MPP microwave drying.
3.2 Effective moisture diffusivity
Table 1 shows the effective moisture diffusivity of MPP. Compared with convective drying, the effective moisture diffusivity of microwave drying increased by 49.2% from 3.01×10-10 m2/s to 4.49×10-10 m2/s. This is because microwaves can penetrate the material directly and generate heat directly inside it, accelerating the diffusion and evaporation of moisture. In contrast, convective drying needs to transfer heat to the surface of the material and undergo heat and mass transfer processes for drying, resulting in a slower diffusion rate.
Table 1.
The effective moisture diffusivity of MPP
| Drying Method | Formula | Deff (m2/s) |
| Convective drying | ln (MR) = -0.0021t + 0.2998 | 3.01×10-10 |
| Microwave drying | ln (MR) = -0.0031t + 0.2169 | 4.49×10-10 |
3.3 Energy consumption
Table 2 shows the energy consumption for convective and microwave drying. According to Table 2, the convective drying time was 22 min and required an energy consumption of 3.90 MJ, while the microwave drying time was 16 min and required an energy consumption of 0.48 MJ. Compared with convective drying, 88% of energy consumption could be saved by microwave drying. This is mainly because microwave drying can directly generate heat within the drying material. In contrast, convective drying necessitates the transfer of a substantial amount of heat to the drying chamber to dry the fabric effectively.
Table 2.
Energy consumption for convective and microwave drying
| Drying Method | Drying Time (min) | Energy Consumption (MJ) |
| Convective drying | 22 | 3.90 |
| Microwave drying | 16 | 0.48 |
3.4 ANN modeling of drying kinetics
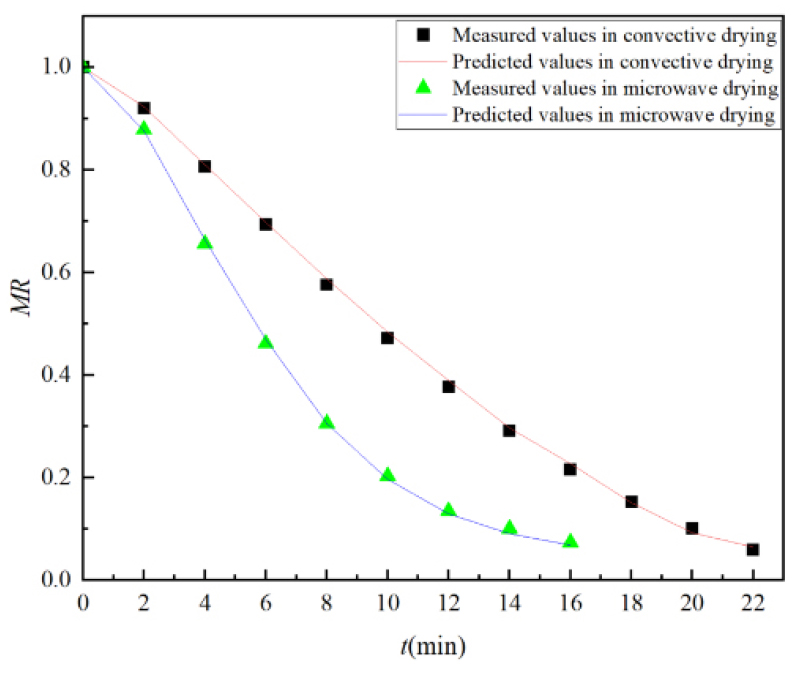
Fig. 3 shows the comparison of measured and predicted moisture ratio of MPP during the convective and microwave drying. As shown in Fig. 3, in the convective drying, the measured values were consistent with the predicted values from 0 to 6 min. From 6 to 16 min, the measured values were slightly lower than the predicted values, while from 16 to 22 min, the predicted values had a slight wave motion. The ANN modeling results showed the RMSE and R2 between the measured and predicted values were 3.28×10-5 and 0.9997 for moisture ratio, respectively, in the convective drying process. Meanwhile, in the microwave drying, the measured moisture ratios were consistent with the predicted values from 0 to 16 min. After 16 min, the measured values were slightly higher than the predicted moisture ratios. Based on modeling results, the RMSE and R2 between the measured and predicted values were 3.16×10-5 and 0.9999 in the microwave drying process. Therefore, the ANN modeling provided a good prediction of the moisture content during the MPP drying process.
4. Conclusions
In this paper, the drying kinetics of MPP in the microwave drying process were investigated experimentally and compared with the convective drying process. The three obvious drying periods were presented in convective drying, i.e., the warm-up rate period, the constant rate period, and the falling rate period. In contrast, only the warm-up and the falling rate period were observed in the microwave drying process. It was found that applying microwave could accelerate moisture diffusion within MPP as the effective moisture diffusivity increased by 49.2%. As a result, the drying time was shortened by 27%. The energy consumption was 3.90 MJ for convective drying versus 0.48 MJ for microwave drying, equal to 88% of energy savings with the microwave method. Finally, the ANN modeling methodology was proved to could simulate the MPP drying kinetics satisfactorily. The results showed that the optimal ANN model has the RMSE and R2 values of 3.28×10-5 and 0.9997 in the convective drying process. Meanwhile, in the microwave drying, the optimal ANN model has the RMSE and R2 values of 3.16×10-5 and 0.9999, respectively. The findings of the current work demonstrated that the ANN modeling could be effectively used to predict drying kinetics and determine the moisture content of the MPP samples.