1. 서 론
2. 재료 및 방법
2.1 공시재료
2.2 표면 프로파일 측정
2.3 표면 거칠음 프로파일 파라미터
2.4 프랙탈 차원 분석
3. 결과 및 고찰
3.1 종이 및 판지의 표면 거칠음 프로파일 파라미터
3.2 종이 및 판지 표면 거칠음도의 프랙탈 차원
3.3 종이 및 판지의 거칠음도 및 프랙탈 차원 간 상관관계
4. 결 론
1. 서 론
물질의 표면 특성에 대한 이해는 제지 산업뿐만 아니라 전자, 의료, 건설 및 석유 산업 등 다양한 산업 분야에 걸쳐 필수적으로 요구된다.1) 프랙탈 기하학은 의료 및 의학 분야의 표면 특성, 다공성 구조, 신호 대 잡음 처리, 센서 및 모니터링 장치 등 여러 영역에서 광범위하게 활용되고 있는 이론으로,2,3,4,5,6) 1961년 Richardson에 의해 제안된 수학적 이론이다. 당시 Richardson은 영국 해안선의 길이를 측정하려고 시도하였으나, 선택한 율척 또는 해상도에 따라 결론이 달라질 수 있다는 사실을 파악하였다.7) Richardson은 측정 분해능이 낮아질수록 해안선의 길이가 증가하는 결과를 통해 유한한 영역 내에서 해안선의 길이가 무한대가 될 수 있다고 주장하였다.
Richardson은 위와 같은 사실을 증명하기 위하여 해안선 길이와 분해능에 대한 관계를 로그-로그 스케일(log-log scale)로 시각화 하였으며 이를 통해 거듭제곱 법칙에 따른 근사적 선형 관계를 도출하였다. Fig. 1은 Richardson이 도시한 해안선의 길이와 분해능 사이의 거듭제곱 법칙에 따른 근사적 선형관계를 나타낸 것이다. Fig. 1의 선형관계는 Eq. 1의 식을 통해 정의할 수 있다. 여기서 C는 상수, a는 기울기, L은 측정 길이, M은 분해능을 의미한다.
이후, Mandelbrot은 Richardson의 문제를 재해석하며, 영국 해안선이 프랙탈 기하학적 특성을 나타내며, Eq. 2의 수식으로 이를 해석할 수 있다고 제안하였다.8) 여기서 a는 기울기를 나타낸다. Eqs. 1, 2에서 확인 가능하듯 기울기 a의 절댓값이 증가하면 해안선 길이 역시 증가하며 이는 해안선의 구조가 보다 복잡한 구조(tortuous)를 지니고 있음을 나타낸다. Fig. 2는 프랙탈 기하학적 구조를 이해할 수 있는 Koch 눈송이 모형을 나타낸 것으로 initiator로 시작해 각 변을 3등분하여 generator를 만드는 과정을 반복함을 통해 눈송이 모양의 프랙탈 기하학적 구조가 나타난다.
프랙탈 차원과 종이 표면 특성 사이의 상관관계는 Eq. 3의 Weierstrass-Mandelbrot 방정식에 표면 거칠음 프로파일 데이터를 대입하여 이해할 수 있다.9,10)
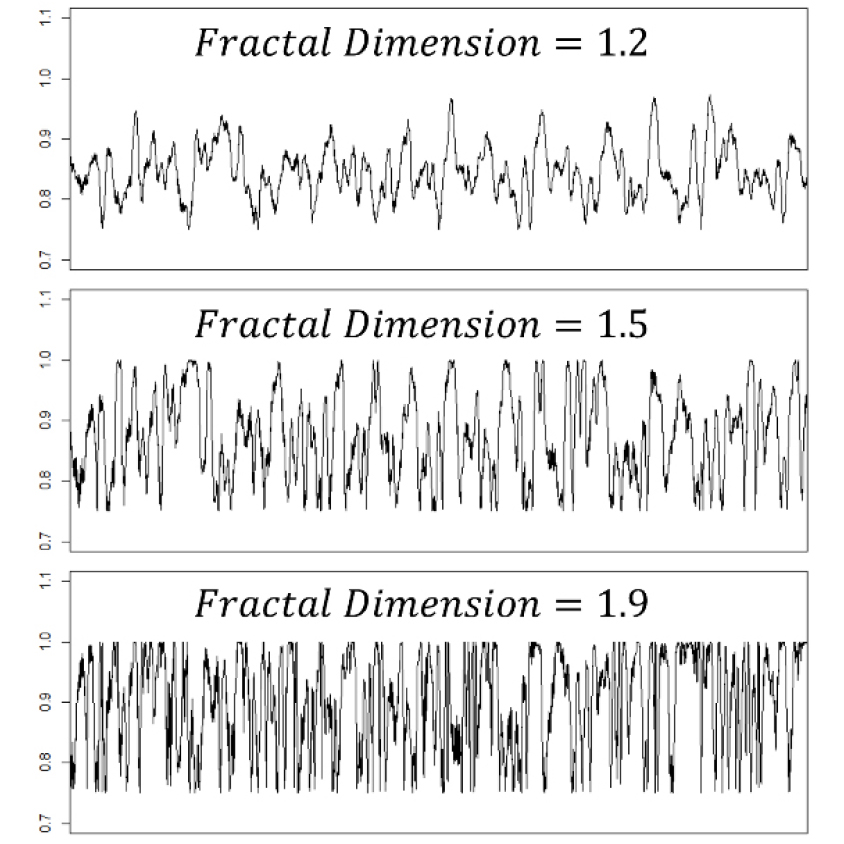
여기서 FD는 프랙탈 차원(Fractal dimension, FD), λ는 평균 높이 혹은 평균 거칠음도, k는 누적된 데이터 포인트 그리고 t는 시계열의 순차 데이터 포인트이다.1)Fig. 3은 λ를 1.5로 설정하여 Eq. 3에 대입하였을 때 생성할 수 있는 동일한 평균 거칠기와 변동계수를 갖으나 서로 다른 FD 값을 보유한 표면 프로파일을 나타낸 것이다. Fig. 3을 통해 FD 값이 증가함에 따라 표면의 거칠기 또는 요철이 증가하는 것을 확인할 수 있다. 이는 서로 같은 평균 거칠기를 가진 표면 프로파일도 FD 값의 차이로 인해 상이한 특성을 나타낼 수 있음을 시사한다. 따라서 표면 거칠음도를 나타내는 평균 거칠기(roughness average, Ra)와 변동계수(coefficient of variance, COV)만을 기반으로 표면 프로파일을 정의할 수 없다고 판단할 수 있다. 이 두 매개 변수는 표면 거칠기를 설명하는 데 일반적으로 사용되지만, 프랙탈 차원 특성을 보유한 표면의 경우, 표면의 복잡성을 반영하지 못할 가능성을 배제할 수 없다.
프랙탈 차원의 관점에서 점은 0, 선은 1, 면적은 2, 부피는 3으로 나타낸다. 따라서 일반적인 유클리드 기하학으로 정의할 수 없는 점, 혹은 선의 넓이 등을 효과적으로 평가할 수 있다. 선도 아니고 면도 아닌 종이의 표면 구조는 1에서 2사이의 프랙탈 차원 값을 보유한다.1,8)
한편, 프로필로메트리(profilometry)는 샘플의 표면 프로파일을 측정하여 표면 특성을 정량 평가하는 기술로 비접촉 방법(non-contact method)과 접촉 방법(contact method)으로 대별할 수 있다.1,11,12,13) 비접촉 방법의 경우 빛을 이용하여 종이 표면을 광학적으로 스캔하여 샘플의 표면과 물리적 접촉이 요구되지 않아 샘플의 변형을 방지할 수 있으며 나노 스케일을 갖는 표면을 특성화 할 수 있다는 장점이 있으나, 적용 영역과 범위가 다소 한정적이라는 단점을 지닌다.14,15)
접촉식 프로필러의 경우 장치에 부착된 탐침(stylus)을 통해 샘플의 표면을 직접 스캔하여 스캔 영역에 대한 높이 프로파일을 생성하며, 이를 표면 거칠음 프로파일로 정의한다.11,13,17) 접촉식 프로필러를 통한 프로파일 추출법의 경우 creping, coating, printing, laminating 등 제지공정 process와 가장 유사한 형태를 취하고 있어 신뢰도가 높은 분석법으로 간주되고 있다.
현재까지 탐침을 통한 접촉 유형의 프로필러를 사용하여 종이 제품의 프랙탈 차원 값을 조사한 연구는 매우 적은 것으로 조사되었다. Militky 등18)은 KES-SE surface tester (Kato Tech., Japan)로 추출한 표면 거칠기 프로파일을 분석하여 부직포(non-woven fabric) 원단 표면의 프랙탈 차원의 계산을 시도하였다. 이를 위해, 변이함수법 (variogram method)1,8,19)을 적용하였으나 데이터 포인트의 한계로 인하여 프랙탈 차원 계산에 실패하였다. 반면 Lee 등20)은 KES-SE surface tester에 데이터 로거(Midi logger GL900, Graptec, Japan)를 부착하여 초당 데이터 수집 개수를 1000개로 증폭하여 코팅 유무에 따른 인쇄용지의 프랙탈 차원 변화와 엠보싱 패턴에 따른 위생용지의 프랙탈 차원을 성공적으로 분석한 바 있다.
본 연구에서는 접촉식 프로필로메트리를 통해 종이 및 판지의 표면 프로파일을 추출하고 프랙탈 기하학적 특성을 파악하여 유클리드 기하학 관점에서 설명이 불가능한 종이의 표면 구조에 대한 정량적 평가 방법을 제시하고자 하였다. 프랙탈 기하학의 원리를 종이 표면 구조 해석에 적용 시 제지 공정에 주로 사용되는 첨가제 및 안료 등과 같은 micro scale 파우더 및 입자들의 성능 예측에 원조할 수 있을 것으로 사료된다.
2. 재료 및 방법
2.1 공시재료
Table 1은 실험에 사용한 종이 시료의 기본 물성을 나타낸 것이다. 표면 특성 분석 시 5종의 시료에 대해 ISO 187에 따라 온도 23±1℃, 상대습도(RH) 50±2% 조건에서 48 h 이상 조습처리한 후 사용하였다.21)
Table 1.
Physical properties of samples
| Sample | Grade | Basis weight, g/m2 | Thickness, mm | Density, g/cm3 |
| R1 | Uncoated P&W | 70.5 | 0.09 | 0.76 |
| R2 | Coated P&W | 117.7 | 0.11 | 1.11 |
| R3 | Newsprint | 46.1 | 0.05 | 0.94 |
| R4 | Liner | 172.0 | 0.24 | 0.71 |
| R5 | Kraft | 79.6 | 0.11 | 0.72 |
2.2 표면 프로파일 측정
종이의 표면 프로파일은 촉침에 의한 직접 접촉이 가능한 표면 시험기(KES-SESRU surface tester, Kato, Japan)를 사용하여 추출하였다.
탐침을 통한 기계적 접촉 방식의 경우 탐침의 직경, 시료와의 접촉각, 접촉힘(contact force), 스캔 속도(scan speed) 등에 따라 거칠음 프로파일의 형상이 변화될 수 있어 보다 정확한 분석을 위해서는 시료에 따라 적합한 조건을 설정할 필요가 있다.13) 본 연구에서는 선행연구를 참조하여 Table 2와 같은 프로파일 분석 조건을 설정하였다.11,12,13,20)
Table 2.
Test conditions for surface roughness characterization
| Contact force, gf | 5 |
| Data acquisition rate, Hz | 1,000 |
| Scan speed, mm/s | 1 |
| Scan length, mm | 20 |
스캔 속도와 데이터 수집 속도는 측정 분해능과 관련된 변수이다.11,12,20)Eq. 4은 각 수집 데이터 포인트 간의 간격(spacing distance, SD)을 나타낸 것이다. Eq. 4에서 L은 총 측정 길이(mm), N은 데이터 포인트를 의미한다.
데이터 포인트는 Eq. 5에 의해 정의될 수 있다. Eq. 5에서 dar은 데이터 수집 속도(Hz)를 나타내며, V는 스캔 속도(mm/s)를 의미한다. 여기서 L/V는 시간(t)을 의미하므로 데이터 포인트는 20,000개(1,000×1×20)가 된다.
Eqs. 4, 5를 종합하면 Eq. 6과 같은 수식이 유도된다. 따라서 20 mm 스캔 길이, 1 mm/s 속도에서 1,000 Hz 데이터 수집속도를 설정할 경우 분해능은 1 μm가 된다.
Fig. 4는 본 연구에서 표면 거칠음 프로파일 추출 시 사용된 탐침의 기하학적 정보를 도시한 것으로 ASTM A681-08:2015에 의거하여 자체 제작하였다. Rtip은 탐침의 직경을 나타내며 본 연구에서는 직경 1 mm의 탐침을 사용하였다.
2.3 표면 거칠음 프로파일 파라미터
종이의 표면 거칠음도 특성 정의를 위한 거칠음 프로파일 파라미터는 거칠기 평균값인 Ra와 거칠기 평균 절대 편차를 나타내는 R-MAD를 측정하여 평가하였다. 거칠기 평균값과 거칠기 평균 절대 편차의 계산식을 Eqs. 7, 8에 나타냈으며, 데이터는 각 시료의 기계 방향(machine direction, MD)에 대하여 각각 10회씩 반복 측정하여 얻은 평균값과 변동계수(coefficient of variation, COV)를 사용하였다. Eqs. 7, 8에서 N은 지정된 스캔 영역에서 데이터 수집 개수를 의미하며 Ri는 지점 i에서의 거칠기를 나타낸다.
Fig. 5는 Ra와 R-MAD를 시각적으로 도시한 것으로 Ra는 추출된 프로파일 높이의 평균을 나타내는 반면 R-MAD의 경우 음영 처리된 영역을 나타낸다.
2.4 프랙탈 차원 분석
본 연구에서는 베리오그램 방법을 이용하여 표면 거칠기 프로파일로부터 종이 표면의 프랙탈 차원을 계산하였다. 베리오그램은 데이터 집합의 공간적 연속성 또는 거칠기를 자기 유사성(autocorrelation)을 분석하는 양적 통계 기술이다. 통계학에서 자기 유사성이란 관찰 값들 간의 종속성을 나타내며, 높은 자기 유사성을 보유한다는 것은 관찰 값들 간의 더 큰 종속성을 나타낸다는 것을 의미한다.
Eq. 9는 베리오그램의 수식을 나타낸 것이며 Fig. 6은 종이(R1)의 표면 거칠기 프로파일 데이터를 Eq. 9에 대입한 결과를 나타낸 것이다. 여기서 lag는 두 점 간의 거리를 의미하며, lag k는 거리가 k인 두 점을 나타낸다. 따라서, k 값이 클수록 두 점 사이의 간격이 크다는 것을 의미하며 각각 와 는 lag k에서의 베리오그램(variogram at lag k), lag k에서의 자기유사성(autocorrelation at lag k)을 나타낸다. 또한 n은 데이터의 개수를 의미한다. 본 연구에서는 SAS JMP 통계 프로그램 times series를 통해 베리오그램 값을 계산하였다.
Fig. 6에서와 같이 Lag와 베리오그램 값에 로그를 취하고 절편이 0인 회귀모델(zero intercept linear regression model)을 작성하면 프랙탈 차원 값을 구할 수 있다. 베리오그램 모델을 통한 프랙탈 차원 값은 Eq. 10에 따라 계산한다.1,20) 여기서 Slope는 작성된 회귀식의 기울기를 의미한다. 결과값은 10회 반복 추출한 프로파일로부터 계산된 프랙탈 차원 값(FD)을 평균하여 도시하였다.
3. 결과 및 고찰
3.1 종이 및 판지의 표면 거칠음 프로파일 파라미터
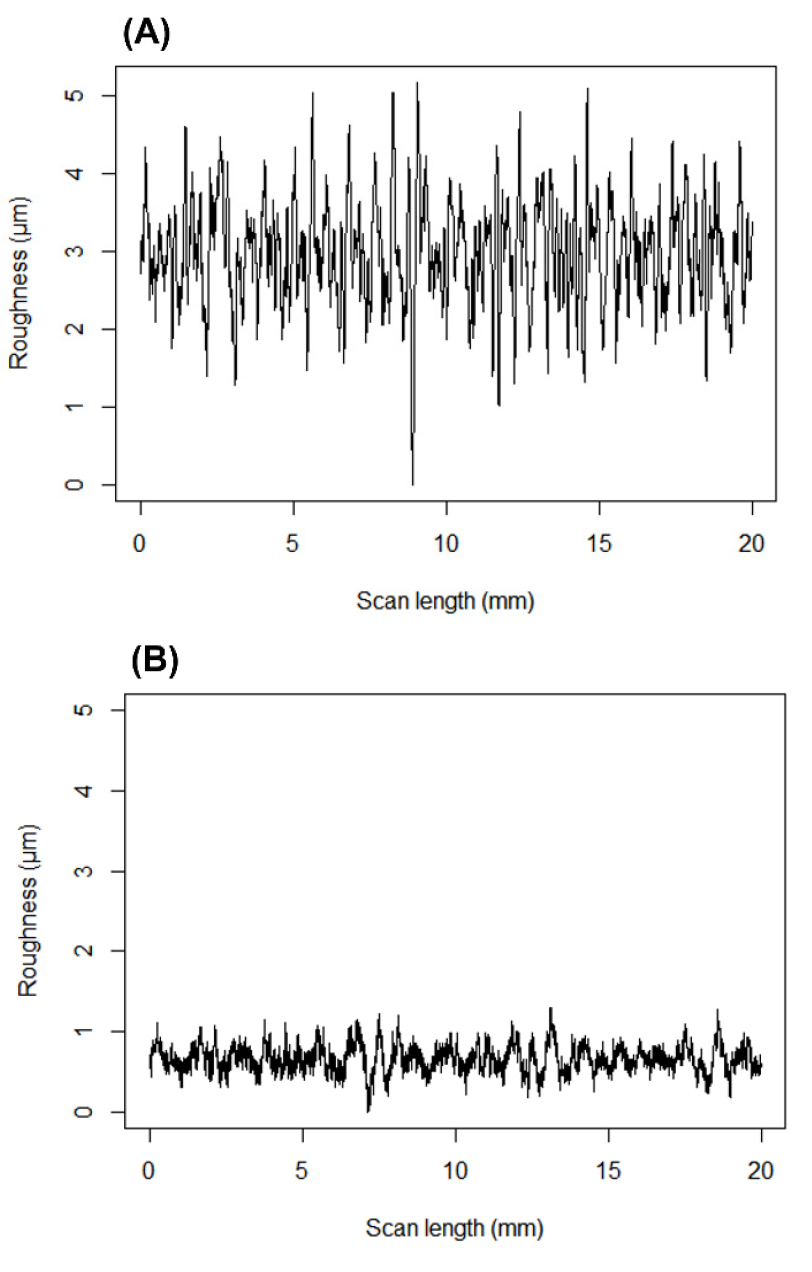
Fig. 7은 코팅 전후 종이의 표면 이미지를 나타낸 것이다. 표면 이미지를 통해 코팅 전후의 표면 특성이 변화된 것을 예측할 수 있다. Fig. 8은 실제 표면 시험기를 통해 추출한 샘플 R1과 R2의 표면 프로파일을 나타낸 것이다. 프로파일 데이터를 통해 코팅이후 평균 거칠기와 거칠기 변동 폭이 감소한 것을 확인할 수 있다. 표면 프로파일 파라미터를 통해서도 이와 같은 사실이 확인 가능하다.
Table 3은 Eqs. 7, 8을 통해 계산한 거칠기 프로파일 파라미터를 나타낸 것이다. R1과 R2를 비교하였을 때 코팅 이후 Ra와 R-MAD가 각각 56%, 4% 감소하였다. 또한 인쇄를 목적으로 제조된 R1-R3의 경우 R4, R5에 비하여 더 낮은 거칠기 특성을 보유한 것으로 분석되었다. 인쇄용지의 경우 잉크의 전이 및 인쇄적성 개선을 위한 도공층 안정성 확보를 목적으로 원지 자체의 불균일성을 최소화하여 제조되는 것으로 알려져 있다.25) 반면 포장을 목적으로 사용되는 라이너지와 크라프트지의 경우 종이 표면에 적정 수준 이상의 불균일성이 부여되어야 마찰 저항력을 통한 stack 불량 문제를 방지할 수 있다.26,27)
한편, Ra의 경우 분석 장비와 측정 조건에 따라 가변성이 매우 높은 파라미터로 보고되고 있다.12,13,20)Table 3에서도 R-MAD와 비교하였을 때 더 높은 변동계수를 기록한 모습을 확인할 수 있다. R-MAD의 경우 Eq. 8에 나타냈듯이 거칠기 평균의 절대 편차를 나타낸다. R-MAD 계산 시 Ra는 단순히 상수로 취급된다. 따라서 Ra에 비하여 R-MAD가 표면 특성을 대변할 수 있는 보다 안정적이고 정밀한 파라미터라고 판단된다.
3.2 종이 및 판지 표면 거칠음도의 프랙탈 차원
Table 4는 종이 및 판지 표면 거칠음도의 프랙탈 차원 값을 나타낸 것이다. 앞서 설명하였듯이 종이 표면 거칠음도의 프랙탈 차원은 1과 2사이의 값을 가지며 1에 가까울수록 요철이 적은 표면으로 해석한다.
샘플 R2의 경우 표면이 코팅 처리된 샘플로서 5가지의 시료 중 가장 낮은 프랙탈 차원 값을 나타내는 것으로 분석되었다. 프랙탈 차원 값의 경우 Table 3의 거칠음 프로파일 파라미터와 전혀 다른 경향성을 나타내고 있다. R4와 R5, 각각 라이너지와 크라프트지의 경우 인쇄를 목적으로 제조된 R1-R3에 비하여 보다 거친 표면을 보유하는 것으로 확인되었다. 따라서 프랙탈 차원 값 역시 2에 가까운 수치를 나타낼 것으로 예상하였으나 이와 같은 경향을 나타내지 않았다. 이는 프랙탈 차원 값이 기존의 유클리드 기하학의 방법론과는 다른 차원의 독립적인 수치임에 따른 결과로 해석된다. 프랙탈 기하학적 특성을 가진 사물의 경우 프로파일 파라미터 만을 통하여 물체의 표면 특성을 정의하기에는 한계가 있을 것으로 사료된다.
Table 3.
Results for surface roughness
| Sample | Ra | R-MAD | ||
|
Avg (μm) |
COV (%) | Avg (μm) |
COV (%) | |
| R1 | 2.23 | 16.8 | 0.54 | 6.6 |
| R2 | 0.51 | 13.5 | 0.12 | 11.0 |
| R3 | 2.24 | 10.7 | 0.55 | 6.7 |
| R4 | 5.29 | 14.1 | 0.79 | 9.9 |
| R5 | 4.15 | 13.5 | 1.01 | 6.5 |
Fig. 9는 R1과 R2의 거칠기 프로파일의 베리오그램을 계산하여 로그를 취한 결과를 나타낸 것이다. 코팅 처리된 R2의 경우 코팅 처리되지 않은 R1에 비하여 변곡점이 보다 빨리 나타난 것을 확인할 수 있다. 이때 절편이 0인 회귀선을 작성하면 R2의 기울기는 R1에 비해 크다. 따라서 R2는 보다 높은 자기유사성을 지닌다고 해석된다. 프랙탈 차원 값의 경우 시료 간 상대비교에는 부적합 할 것으로 예견되나 코팅, 인쇄, 엠보싱 등 동일 시료내 가공공정에 따른 표면 특성 변화를 관찰하기 위한 파라미터로는 적용이 가능할 것으로 사료된다.
3.3 종이 및 판지의 거칠음도 및 프랙탈 차원 간 상관관계
Fig. 10은 R-MAD와 Ra를 비교한 결과를 나타낸 것이다. 결정계수(R2)가 0.78로 나타난 것으로 보아 두 파라미터 간 상관성은 유의하다고 해석할 수 있으나 기울기의 경우 0.158로 1이하의 낮은 기울기를 나타내고 있다. 이는 Ra의 변동성이 R-MAD에 비하여 상대적으로 큰 것을 의미한다. 따라서 측정 장비와 분석 조건에 따라 가변적인 Ra에 비하여 R-MAD가 보다 정확한 표면 정보를 반영할 수 있을 것으로 판단된다.1,11,12,20)
Fig. 11은 프랙탈 차원과 거칠음 프로파일 파라미터를 비교한 결과를 도시한 것이다. Ra와 R-MAD 모두 프랙탈 차원과 유의미한 상관성을 나타내지 않는 것으로 분석되었다. 이는 프랙탈 차원이 기존의 유클리드 기하학과는 다른 차원을 갖는 독립적인 파라미터임에 기인된 결과로 해석된다.
4. 결 론
본 연구로부터 도출된 결론은 다음과 같다.
1)표면 프로파일 추출 시 1 mm/s의 스캔 속도, 1000 Hz의 데이터 수집 속도에 따른 1 μm의 분해능의 설정은 프로파일 파라미터와 프랙탈 차원 계산을 위한 적합 조건이라 판단된다.
2)R-MAD는 측정 장비와 분석 조건에 따라 가변적인 Ra에 비하여 시료의 표면 특성을 대변하기 위한 보다 안정적인 파라미터로 해석된다.
3)프랙탈 차원 값의 경우 동일 시료 내 가공공정에 따른 표면 특성 변화 평가 시 유용하게 적용될 수 있을 것으로 기대된다.
4)프랙탈 차원의 경우 유클리드 기하학으로 설명하기 어려운 사물의 특성을 효과적으로 평가할 수 있는 유용한 파라미터이며, 종이의 표면 특성 분석에 적용할 수 있을 것으로 판단된다.
이상의 결론을 통해 프랙탈 차원 개념의 도입은 종이 및 판지의 표면 특성 해석 및 거칠음도 특성의 정량적 분석에 새로운 방향성을 제시할 수 있을 것으로 판단된다.