1. 서 론
2. 재료 및 방법
2.1 공시재료
2.2 데이터 세트
2.3 주성분 분석과 밀도 기반 클러스터링을 통한 이상치 탐지
2.4 랜덤포레스트 회귀 모델
2.5 IR 스펙트럼 데이터의 변수 중요도 분석
2.6 회귀 모델의 평가
2.7 회귀 모델의 비교
3. 결과 및 고찰
3.1 셀룰로오스 아세테이트의 적외선 분광학적 특성
3.2 밀도 기반 클러스터링을 통한 IR 스펙트럼 데이터의 이상치 탐지 및 주성분 분석
3.3 랜덤포레스트를 이용한 셀룰로오스 아세테이트의 치환도 예측 모델링
3.4 셀룰로오스 아세테이트의 치환도 예측을 위한 스펙트럼 변수 중요도
3.5 셀룰로오스 아세테이트의 치환도 예측을 위한 모델 성능 비교
4. 결 론
1. 서 론
셀룰로오스 아세테이트(cellulose acetate, CA)는 1865년 Schutzenberg1)에 의해 최초로 제조된 에스테르화(esterification) 셀룰로오스 유도체로서, 초기에는 180°C의 가혹한 반응조건으로 인하여 결정구조 붕괴 혹은 분자량 감소와 같은 현상이 빈번히 발생하여 활용 범위가 제한되었다. 이후 Eichengrün과 Theodore Becker에 의해 처음으로 가용성 셀룰로오스 아세테이트가 발명되었다.2) CA는 황산(sulfuric acid)을 촉매로 하여 셀룰로오스를 무수 아세트산(acetic anhydride)과 반응시켜 제조된다.3) 기존의 CA를 제조하기 위한 원료로는 주로 면(cotton) 혹은 용해용 펄프(dissolving pulp)가 이용되었으나 최근에는 재활용 종이자원,4) 볏짚5) 및 대나무6)등 다양한 자원들이 검토되고 있다.
CA는 주로 치환도(degree of substitution, DS)에 따라 품질과 용도가 좌우되며, 용매의 선택도 치환도에 따라 달라진다. 일반적으로 용매의 경우 DS 1.2–1.8 범위에서는 2-메톡시 에탄올(2-methoxyethanol),7) 2.2–2.7 범위에서는 아세톤(acetone)8) 그리고 2.8–3.0 범위에서는 클로로포름(chloroform)9)이 사용된다. CA는 섬유, 필름, 필터, 의공학 소재, 포장재 등 다양한 산업군에 재료로서 활용되고 있다.3) CA의 DS 측정법으로서 가장 일반화된 방법은 아세틸화된 시료를 페놀프탈레인과 산을 통해 적정하고 아세틸기 함량을 분석한 뒤 이를 수식에 대입하는 방법이다.10)그러나 상기 과정의 경우 많은 시간이 소비되며, 분석 과정이 노동 집약적이고 실험자에 의한 오차 발생율이 상대적으로 높아 이를 개선하기 위한 연구들이 다수 보고되고 있다.
Fei 등11)은 치환도가 서로 다른 상용 CA와 셀룰로오스의 적외선 분광분석(infrared spectroscopy, IR)을 수행하여, 아세틸기(acetyl group)로부터 유래된 유효 피크 강도(intensity)와 면적(integral area)을 통해 표준 오차 2.31%의 CA 치환도 분석 모델을 구축한 바 있다. Wolfs 등12)은 아세틸기 유래 IR 피크와 hydrogen-1 nuclear magnetic resonance spectroscopy(1H NMR) 분석 결과의 비교를 통하여 결정계수(coefficient of determination, R2) 0.958과 0.998의 회귀식을 작성하였다. 이 밖에도 CA의 DS 분석 한계를 극복하고자 gas chromatography-mass spectrometry(GC-MS),13) ultraviolet-visible spectroscopy (UV-Vis spectroscopy)14) 및 원소 분석(elemental analysis)15)의 활용이 검토된 바 있다. 현재까지 검토된 방법의 경우 CA의 DS를 분석함에 있어 파괴적인 시험방법이 요구되거나 정밀도와 재현성에 있어 한계가 있는 것으로 파악된다. 특히 단순히 IR 피크의 intensity를 기반으로 작성한 DS 분석 모델의 경우 특정 IR 피크가 다른 화학적 특성과 중첩되거나 시료 준비 과정에서 발생하는 변동성에 의해 정밀도가 제한될 수 있다.
최근에는 이러한 분석 장비를 통해 도출된 재료의 물리화학적 정보에 화학계량학적(chemometrics) 방법을 접목하여 재료의 특성을 보다 정밀하게 분석하는 시도가 이루어지고 있다. 특히 기계학습(machine learning)의 발전은 화학계량학의 확장을 유도하였으며, 제지 분야와 셀룰로오스 재료의 특성화에 있어서도 이의 유효성이 검증된 바 있다.16,17,18) CA의 DS 분석을 위해 기계학습 방법이 적용된 선행연구에서는 partial least square-discriminant analysis(PLS-DA), support vector machine(SVM) 및 K-NN(k-nearest neighbor) 등의 모델과 적외선 분광법을 결합하여 분류 모델링(classification modeling)이 수행된 바 있다.19) 그러나 분류 모델은 데이터가 사전에 정의된 범주 내에 속하는지를 예측하는 데 적합한 방식으로, DS와 같이 연속적인 값을 가지는 데이터 세트를 정확하게 반영하기에는 한계가 있다. 이러한 점에서, 보다 정밀한 DS 분석을 위해서는 연속 변수의 특성을 효과적으로 반영할 수 있는 회귀 모델링(regression modeling) 접근법이 필요하다.
본 연구에서는 CA의 DS 예측 모델링에 있어 회귀 모델링 접근을 도입하여, 적외선(IR) 스펙트럼 데이터를 기반으로 랜덤 포레스트(random forest, RF), partial least squares regression(PLSR), 다층 퍼셉트론(multilayer perceptron, MLP) 모델을 구축하고, 각 모델의 예측 성능을 평가하였다. 특히, RF 모델 학습 과정에서 도출된 변수 중요도(feature importance) 정보를 활용하여 IR 스펙트럼에서 입력 변수로 사용할 최적의 범위를 재설정하였다. 이를 통해 기존 적정법의 한계를 보완하고, 실험적 오차를 최소화하며 분석 효율성을 향상시킬 수 있는 새로운 셀룰로오스 아세테이트의 치환도 분석 방법을 제시하고자 한다.
2. 재료 및 방법
2.1 공시재료
DS 예측 모델링을 위한 CA 원료에 대한 정보를 Table 1에 도시하였다. 사용된 CA는 활엽수 표백 크라프트 펄프를 원료로 분말상으로 제조되었으며, 상세 정보는 Lee 등19) 이 보고한 연구에서 확인할 수 있다. DS의 조절은 증류수 300 mL에 제조된 CA를 투입하고 0.5M 수산화 소듐(Sodium hydroxid, Daejung Chemical, Republic of Korea) 수용액 315 mL를 추가하여 반응시간에 따라 탈아세틸화(deacetylation) 처리하여 진행하였다. 별도의 처리를 진행하지 않은 활엽수 표백 크라프트 펄프 원료의 경우 DS0.00으로 명명하였다.
Table 1.
DS values of cellulose acetate19)
탈아세틸화가 완료된 CA 0.1 g에 0.25M 수산화 소듐 수용액 5 mL, 에탄올 5 mL를 혼합하여 24시간 동안 교반하였다. 이 후 0.25 M 염산 수 용액 10 mL를 첨가하여 30분 동안 반응시킨 후, 페놀프탈레인(Phenolphthalein, Sigma Aldrich, United States) 지시약을 투입하여 CA 용액이 무색에서 분홍색으로 변할 때까지 0.25M 수산화 소듐 수용액으로 적정하였다. 상기 적정법으로 측정한 DS를 예측 모델링을 위한 종속 변수로 사용하였다.
2.2 데이터 세트
2.2.1 셀룰로오스 아세테이트의 적외선 분광분석
셀룰로오스 아세테이트의 적외선 스펙트럼 데이터는 FT-IR(Fourier transform infrared spectroscopy, Frontier Model, Perkin Elmer, United States)을 이용하여 ATR(attenuated total reflection) 모드로 4000–400 cm-1 파장범위에서 4 cm-1 간격으로 측정하였으며, 최종 데이터는 16회 반복 측정에 대한 평균치를 사용하였다. 데이터 세트는 IR 스펙트럼을 시료 당 10회 반복 측정하여 총 100개로 구성하였다.
2.2.2 IR 스펙트럼 데이터 전처리
데이터 세트 내의 IR 스펙트럼은 Savitzky-Golay 필터20)를 이용하여 3차 다항식으로 2차 미분하였다. 이때 평활화 필터의 크기는 27 point로 설정하였다. 평활화 필터의 크기가 클수록 노이즈 제거에 유리하지만 지나치게 큰 필터 사이즈의 설정은 원본 스펙트럼의 신호를 왜곡시킬 수 있어 상기와 같은 조건을 설정하였다. IR 스펙트럼의 2차 미분 전처리는 스펙트럼의 baseline을 보정하고 유효피크의 증폭을 유도할 수 있다.21)
측정된 원본 IR 스펙트럼과 2차 미분 스펙트럼은 Eq. 1에 의거하여 L2 정규화(L2 normalization) 처리 이후 예측 모델링을 위한 데이터로 사용하였다. Eq. 1에서 는 정규화 할 IR 스펙트럼 데이터를 나타내며 는 의 번째 데이터 포인트, 그리고 n은 IR 스펙트럼 데이터의 개수를 의미한다.
2.2.3 데이터 세트 분할
셀룰로오스 아세테이트의 DS 예측 모델링을 위한 IR 스펙트럼 데이터 세트는 7:3의 비율로 모델 학습에 사용될 훈련 데이터 세트(train set)와 예측 성능 평가에 사용될 테스트 데이터 세트(test set)로 분할하였다. 데이터 분할은 모집단의 데이터 분포 비율을 유지하기 위해 층화표집(stratified random sampling) 방법을 사용하였다. 그러나 IR 데이터는 동일 샘플에서 반복 측정된 데이터가 포함되어 있어 반복 데이터 간 높은 상관성이 발생할 가능성이 크다. 이러한 특성은 훈련 데이터 세트와 테스트 데이터 세트 간의 정보 누설(data leakage)을 초래할 수 있으며, 결과적으로 모델의 예측 성능이 과대평가될 위험이 있다. 이를 방지하고 모델 성능 평가의 신뢰성을 확보하기 위해, 7:3으로 분할된 데이터 세트를 기반으로 3겹 교차검증(3-fold cross-validation)을 수행하여 훈련 및 테스트 데이터 간의 상관성을 최소화하고 모델의 성능을 평가하였다.
2.3 주성분 분석과 밀도 기반 클러스터링을 통한 이상치 탐지
셀룰로오스 아세테이트의 치환도 변화에 따른 IR 스펙트럼의 변화를 관찰하고자 주성분 분석(principal component analysis, PCA)을 수행하였다. PCA는 고차원의 IR 데이터 세트에 숨겨진 구조와 패턴을 탐색하는 데에 유용하다고 보고된 바 있다.22,23)PCA 분석을 통해 7,049 차원으로 구성된 IR 스펙트럼 데이터는 10개의 주성분(principal component, PC)으로 구성된 직교 좌표계에 투영된 이후 설명력이 높은 PC를 이용하여 2차원의 형태로 시각화 하였다.
데이터 세트 내에 존재하는 이상치(outliers)는 모델의 정확도와 일반화 성능을 저하시킨다.18) 구성된 IR 스펙트럼 데이터 세트에 포함된 이상치를 검출하고자 밀도 기반 클러스터링(density-based spatial clustering, DBSCAN)을 통해 PC 직교 좌표계에 투영된 데이터 포인트에 대한 이상치 탐지를 수행하였다. DBSCAN에서 클러스터의 반경과 클러스터를 이루는 개체의 최솟값을 나타내는 매개변수인 epsilon(eps)과 minPts는 각각 0.03과 5로 설정하였다. 상기의 설정은 DBSCAN 모델이 하나의 데이터 포인트에서 0.03 거리 이내에 있는 5개 이상의 연속적인 포인트를 하나의 클러스터로 인지하도록 작동함을 나타낸다.
2.4 랜덤포레스트 회귀 모델
RF(Random Forest)는 앙상블 학습(ensemble learning) 기법을 활용하는 예측 모델로, 주어진 학습 데이터셋을 기반으로 다수의 예측 모델을 생성하여 그 결과를 종합함으로써 예측 정확도를 향상시킨다.24) RF는 앙상블 학습 절차에 따라 다수의 결정 나무(decision tree, DT)를 생성한 후, 개별 DT의 예측 결과를 종합하여 최종 예측을 수행한다.
RF는 학습 과정에서 반복적인 무작위 표본 추출(bootstrapping)과 변수 선택을 통해 다수의 DT를 생성하며, 새로운 클래스에 대한 예측은 이렇게 생성된 여러 DT의 예측을 종합하여 이루어진다. 이러한 표본 추출 방법에 기반한 예측 결과 종합 방식은 배깅(bagging, bootstrap aggregating)이라 한다.25) RF는 배깅을 기본 원리로 하며, 무작위 표본 추출과 변수 선택 과정을 추가하여 과적합(overfitting) 가능성을 최소화하고 모델의 일반화 성능을 향상시킨다.
RF 모델은 학습 과정에서, 훈련 데이터셋으로부터 n개의 클래스를 복원 추출 방식으로 반복하여 추출하여 DT를 생성한다. 이 복원 추출 과정에서 일부 클래스는 DT 생성에 사용된 표본에 포함되지 않는데, 이를 OOB(out-of-bag) 데이터라 한다. OOB 데이터는 DT의 검증에 사용된다. 생성된 각 DT는 전체 변수 중 노드 분할에 사용할 변수(n_feature)를 선택하며, n_feature는 모든 노드에 대해 동일하게 적용된다.
본 연구에서는 RF 모델 구축 시 base learner로 CART(classification and regression tree) 알고리즘을 기반으로 한 DT를 사용하였다.26) DT 생성을 위한 n_feature는 전체 입력 변수의 제곱근(‘sqrt’), 이진 로그(‘log2’), 그리고 삼분의 일(‘1/3’)로 각각 설정하였다. 또한, RF를 구성하는 DT의 개수(n_tree)는 초기 10–300개로 설정하였으며, 이후 최종 매개변수는 최소 OOB 오류를 기준으로 선정하였다.
2.5 IR 스펙트럼 데이터의 변수 중요도 분석
RF는 모델 내의 각 DT의 학습과정으로부터 입력 변수에 대한 중요도 정보를 산출한다. 본 연구에서는 DT의 노드 분할에 사용된 입력 변수의 불순도 감소량(mean decrease impurity, MDI)을 기준으로 IR 스펙트럼 변수의 중요도를 계산하였다.27) 개별 DT는 목표 변수(종속 변수)와 입력 변수(독립 변수) 간의 오차(residual error) 감소를 최대화하는 방향으로 노드 분할을 수행한다. 노드 분할 이후 오차 감소가 클수록 해당 입력 변수는 목표 변수에 강한 설명력을 가지며 데이터셋을 더 잘 분리하고 있다는 것을 의미한다. 예를 들어, 특정 노드 분할 이후 생성된 서브셋의 오차 감소량이 0이라면 해당 입력 변수와 분할점의 선택이 모델 성능에 기여하지 않았음을 나타낸다. 반대로, 오차 감소량이 높다면 해당 입력 변수와 분할점의 선택이 모델 성능에 유의미하게 기여했음을 의미하며, 이는 해당 변수의 예측 중요도가 높다는 것을 시사한다. RF 모델은 이러한 오차 감소량을 종합하여 입력 변수의 상대적 중요도를 평가하며, 이를 통해 각 변수의 회귀 모델에서의 기여도를 정량적으로 산출할 수 있다.
2.6 회귀 모델의 평가
셀룰로오스 아세테이트의 치환도 예측에 대한 RF 모델의 예측 성능은 Eq. 2 및 Eq. 3에 나타낸 결정계수(coefficient of determination, R2)와 평균 제곱근 오차(root mean square error, RMSE)를 통해 평가하였다. 여기서 와 는 각각 번 째의 측정된 DS와 예측된 DS를 나타내며, 𝜇는 전체 평균, 은 전체 측정값의 개수를 의미한다.
2.7 회귀 모델의 비교
RF 모델의 예측 성능을 비교하기 위하여 동일한 데이터 세트로 PLSR과 MLP 모델을 구축하여 예측 정확도를 평가하였다. PLSR의 매개변수인 PLS factor의 최대 개수는 초기 10개로 설정하였다. 이후, 3겹 교차 검증(3-fold cross validation)과 격자 검색을 수행하여 최소 RMSE를 기반으로 PLS factor의 최적 개수를 결정하였다.
MLP 회귀 모델은 역전파(backpropagation) 기능을 통해 학습되었으며, 출력층(output layer)에는 별도의 활성화 함수(activation function)를 적용하지 않았다. 손실 함수(loss function)로는 제곱 오차(squared error)가 사용되었고, 손실함수에 대한 최적화는 확률적 경사 하강법(stochastic gradient descent)에 기반한 최적화 기법인 SGD와 Adam을 적용하였다. 초기 학습률은 0.0001, 0.001, 0.01, 0.1의 범위로 설정하였으며 최대 반복 횟수(epoch)는 1000번으로 지정하였다. MLP의 은닉층(hidden layer)에는 16, 32, 64, 128, 256, 512개의 노드 구성을 적용하여 다양한 네트워크 구조(network architectures)를 테스트하였다. 최종 매개변수와 네트워크 구조는 격자 검색을 수행하여 최소 오차를 기준으로 결정하였다.
이상의 데이터 처리와 예측 모델링은 R software(R Core Team, ver. 4.4.1, Auckland, New Zealand)와 오픈 소스 라이브러리를 통해 수행하였다.
3. 결과 및 고찰
3.1 셀룰로오스 아세테이트의 적외선 분광학적 특성
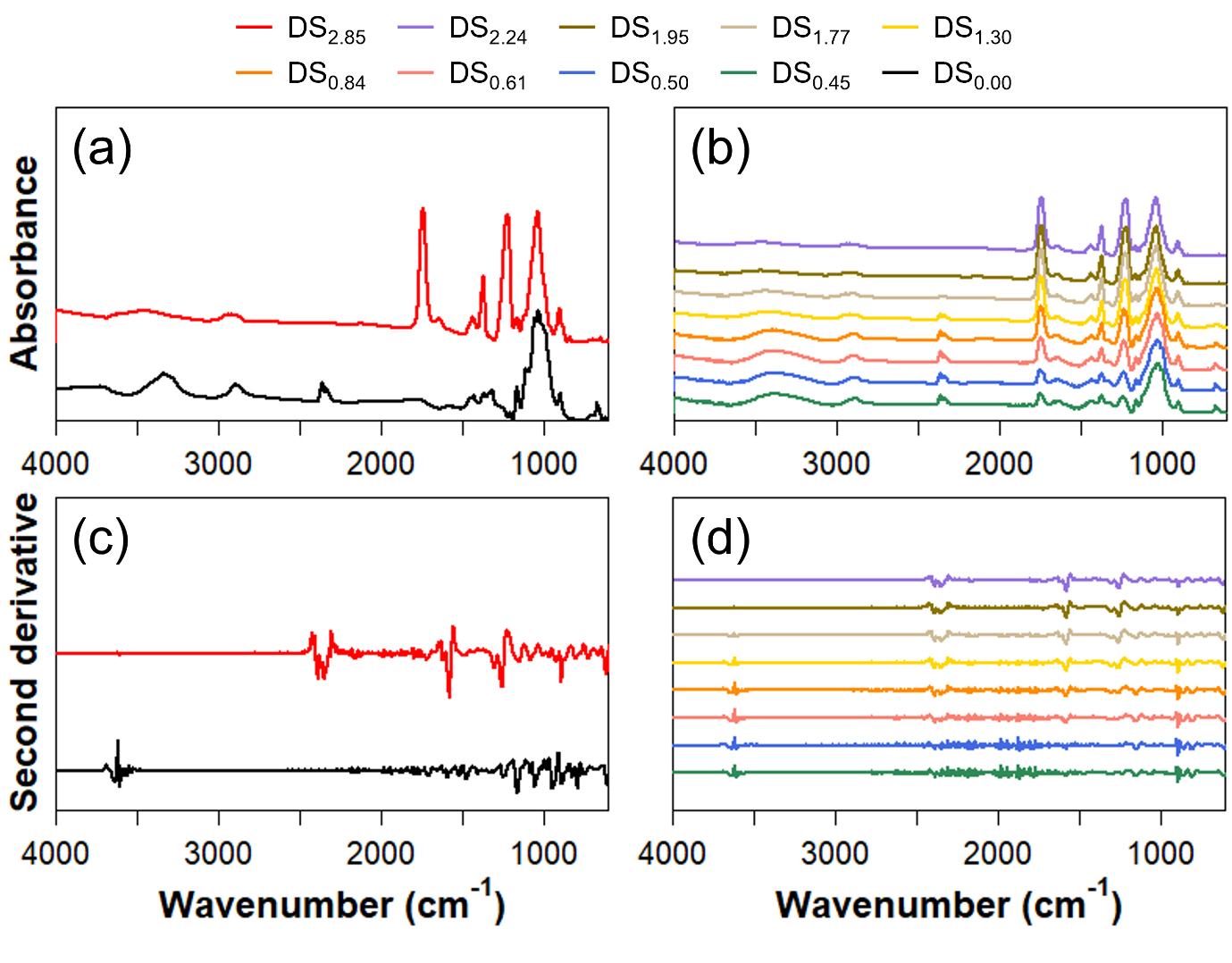
Fig. 1은 CA 제조를 위해 사용된 원료(Hw-BKP)와 제조된 CA의 IR 스펙트럼 데이터를 나타낸 것이다. Fig. 1a 나타낸 원료의 IR 스펙트럼의 경우 3400 cm-1(-OH stretching)과 1050 cm-1(C-O-C in anhydroglucose units)흡수대에서 강한 피크를 나타내었다. 한편 DS 2.85의 CA에서는 1750 cm-1(C=O stretching of the acetyl group), 1370 cm-1(C-H bending vibration of CH3 in the acetyl group), 1240 cm-1(C-O stretching of the acetyl group)에서 특징적인 피크를 나타냈으며, 3400 cm-1 흡수대 부근에서는 아세틸화의 영향으로 피크의 강도가 감소한 것을 확인할 수 있었다.11)
Fig. 1b는 탈아세틸화 처리에 따른 IR 스펙트럼 변화를 도시한 것인데, 탈아세틸화 처리 시간이 증가함에 따라 아세틸기 함량이 감소한 영향으로 1750 cm-1(C=O stretching of the acetyl group), 1370 cm-1(C-H bending vibration of CH3 in the acetyl group), 1240 cm-1(C-O stretching of the acetyl group)에서의 피크 강도가 약화되는 것을 확인할 수 있었다.12)
Fig. 1c와 Fig. 1d는 각각 Fig. 1a와 Fig. 1b의 원본 스펙트럼을 2차 미분한 스펙트럼을 나타낸 것이다. 원본 스펙트럼에 비하여 1200–900 cm-1(cellulose fingerprint)28) 흡수대 부근에서 다수의 피크가 식별되었으나 아세틸기와 관련된 추가적인 정보는 확인되지 않았다. 또한 원본 스펙트럼에 포함된 노이즈 역시 함께 증폭되어 유효하지 않은 피크 역시 다수 관찰되었다.
3.2 밀도 기반 클러스터링을 통한 IR 스펙트럼 데이터의 이상치 탐지 및 주성분 분석
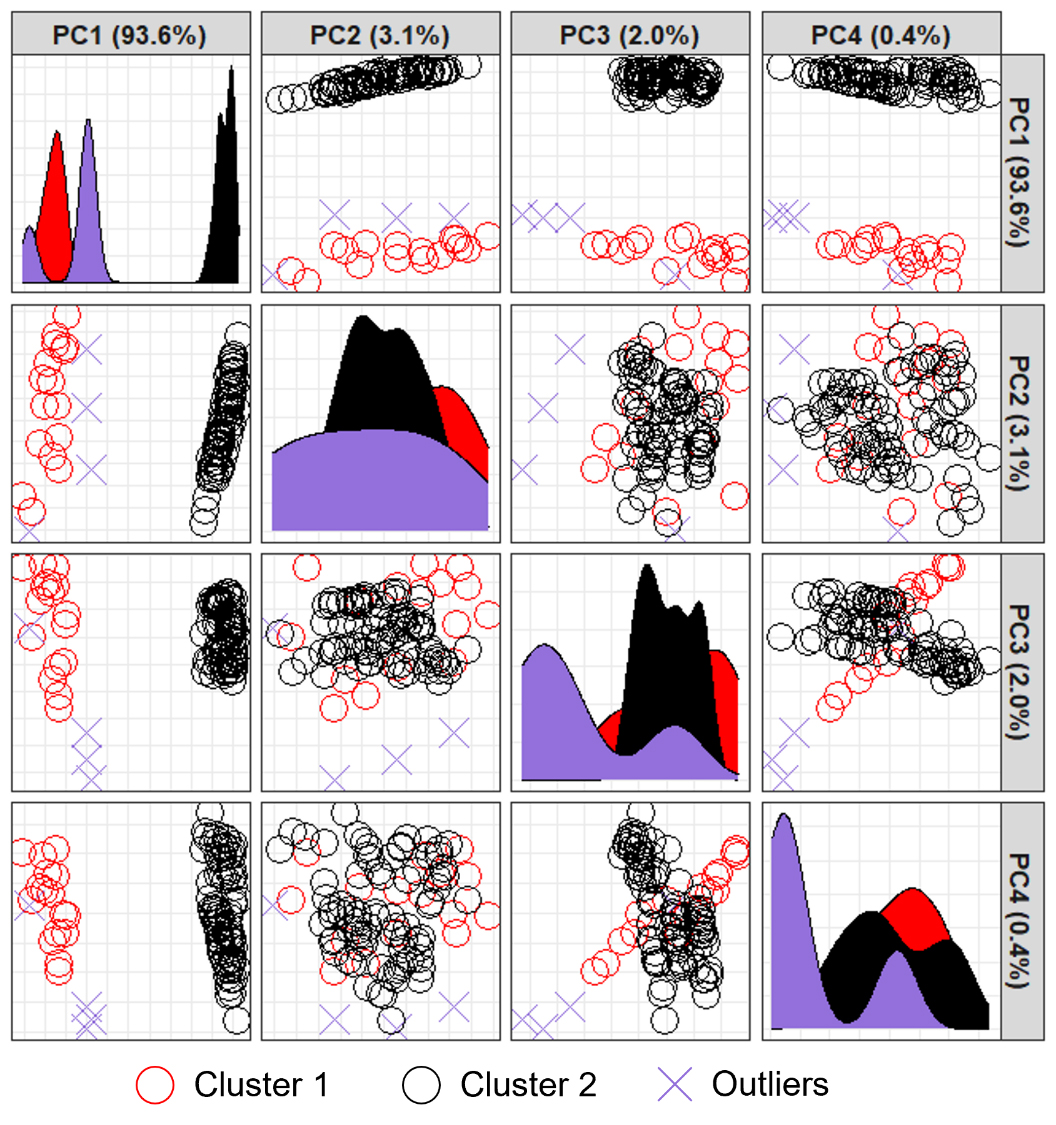
Fig. 2는 밀도 기반 클러스터링을 통한 이상치 탐지 결과를 주성분 분석을 이용하여 시각화 한 것이다. PCA는 다차원 데이터의 패턴과 변동성을 요약하여, 데이터의 주요 구조를 설명할 수 있는 PC를 생성한다. 주성분 분석의 결과로 생성된 각 PC는 IR 스펙트럼 데이터셋의 군집 구조를 2차원 공간에 시각화하기 위해 사용된다. Fig. 2에서 각 축의 괄호 안에 표시된 숫자는 해당 PC가 설명하는 분산의 비율을 의미하며, 데이터의 주요 특징에 대한 설명력(explanatory power)을 나타낸다.
DBSCAN은 데이터 밀도를 기반으로 군집(cluster)을 형성하고, 특정 밀도 조건을 충족하지 못하는 데이터 포인트를 이상치로 간주하는 알고리즘이다. Fig. 2의 결과는 2차 미분 스펙트럼 데이터셋을 사용하여 분석한 결과를 나타낸 것으로, 이 데이터셋에서 DBSCAN 수행 결과 두 개의 군집이 형성되었음을 확인하였다. 또한, 군집에 속하지 못하고 이상치로 탐지된 데이터 포인트는 총 4개였으며, 모두 DS2.85에 해당하는 데이터로 확인되었다.
이와 대조적으로, 원본 스펙트럼 데이터에서는 어떠한 이상치도 탐지되지 않았다. 이는 2차 미분 스펙트럼이 데이터의 세밀한 차이를 강조함으로써 이상치를 보다 잘 탐지할 수 있었음을 시사한다.21,29)
이상치의 존재 여부가 모델의 예측 성능에 미치는 영향은 이후 RF 모델링 과정을 통해 검토하였다. 이를 통해 이상치를 제거하거나 포함하는 데이터셋이 회귀 모델의 성능에 미치는 영향을 분석하고자 하였다.
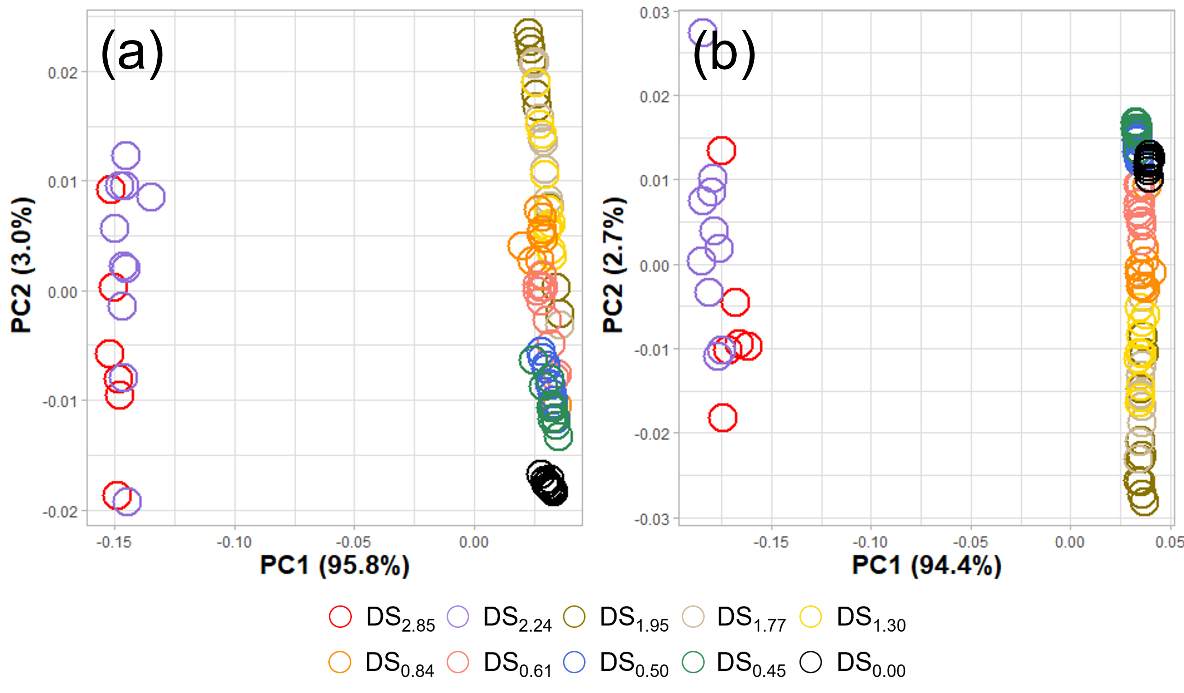
Fig. 3은 CA의 고차원 IR 스펙트럼으로부터 변환된 PC 중 최대 분산을 나타내는 PC1과 PC2를 이용한 2차원 시각화 결과이다. PC score plot(Fig. 3)에서는 Fig. 2에서 검출된 이상치에 해당하는 데이터 포인트를 데이터 세트로부터 제거하였다. Fig. 2의 pair plot으로부터 확인된 CA의 IR 스펙트럼 데이터 세트 내 군집은 총 2개였다. 이상치가 제거된 PC score plot에서도 이와 같은 특성을 나타냈으며 서로 다른 군집은 DS 2.0을 기준으로 형성된 것으로 확인되었다. 이는 셀룰로오스의 아세틸화 과정에 있어 반응 속도의 차이에 따른 CA의 구조 차이에 기인한 결과로 사료된다. Heterogeneous acetylation의 경우 아세틸화 과정에서 반응에 참여한 셀룰로오스는 초기 단계에서 반응 시스템 내에 용해되지 않고 분산된다. 에스테르화는 셀룰로오스 표면이나 팽창한 비결정 영역에서 일어나며, 이로 인해 반응에 참여하는 -OH의 농도가 아세트산 무수물(Ac2O)의 농도보다 낮아진다. 이때 -OH의 농도가 아세틸화 속도의 결정 인자가 되며, 반응 속도는 -OH 농도에 비례한다.11,30) 그러나 DS 값이 2.0을 초과하여 CA의 용해도가 증가하면 반응 시스템은 균질화(homogenization)되며, -OH와 아세트산 무수물의 소모가 동일하게 이루어져 -OH와 아세트산 무수물 농도의 비가 1로 유지된다. 따라서 아세틸화 속도 상수는 -OH 농도와 아세트산 무수물 농도의 곱에 비례하게 되며, 이는 DS 값이 2.0 이상일 경우 아세틸화가 2차 반응 속도론에 대응되는 homogeneous acetylation으로 진행됨을 의미한다.11,12,31)
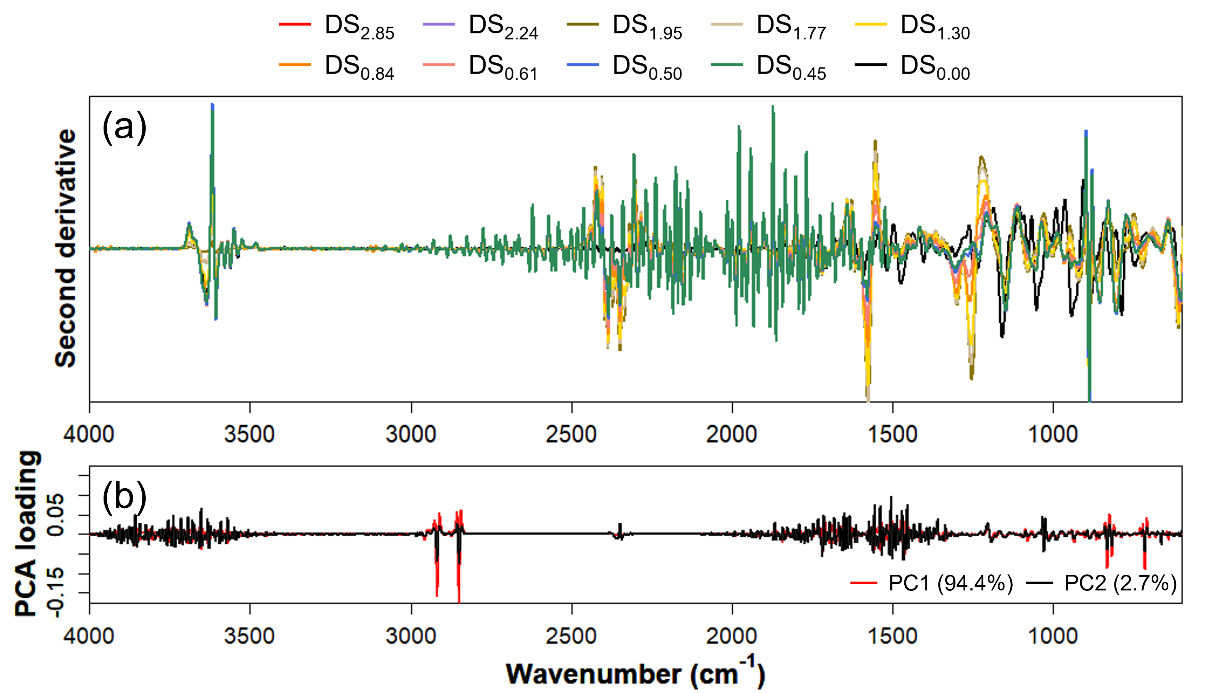
Fig. 4는 CA의 치환도에 따른 2차 미분 IR 스펙트럼과 그에 대응하는 PC 로딩값을 도시한 것이다. Fig. 3에 제시된 비교적 뚜렷한 군집화 특성으로 인하여 제시된 PC 로딩값을 통해 CA의 치환도에 따른 PC에 대한 변수들의 영향력을 확인할 수 있을 것이라 기대하였다. 그러나 PC 로딩값으로부터 아세틸화 과정에서 유래된 피크를 명확히 식별하기 어려웠으며 충분한 군집화 특성에 대한 논리적 근거를 제공하지 못하는 것으로 나타났다. 이는 정제되지 못한 노이즈의 지배적 영향에 따른 결과로 사료된다. 특히, IR 스펙트럼 2700–1900 cm-1 영역의 경우 측정과정에서 CO2 혹은 스펙트럼의 baseline 조정과 background 조정에 따라 야기되는 노이즈와 유용하지 않은 정보들을 포함할 가능성이 높다.32) 따라서, 군집화 특성을 보다 명확히 식별하기 위해서는 해당 영역의 변수에 대한 선택적 적용 또는 제외가 필요할 것으로 판단된다.
또한 선형(linear) 조합으로 구성된 PCA의 특성상 2개의 PC만을 통해 heterogeneous acetylation과 homogeneous acetylation과 관련된 데이터 포인트들이 모두 포함된 데이터 세트의 구동력을 설명함에 있어 한계점이 있는 것으로 판단된다.33) 따라서 전범위의 DS를 분석하기 위한 도구로는 보다 고차원의 특성 반영이 가능하며 데이터 세트의 비선형 특성을 고려할 수 있는 모델이 적용되어야 할 것으로 사료된다.
3.3 랜덤포레스트를 이용한 셀룰로오스 아세테이트의 치환도 예측 모델링
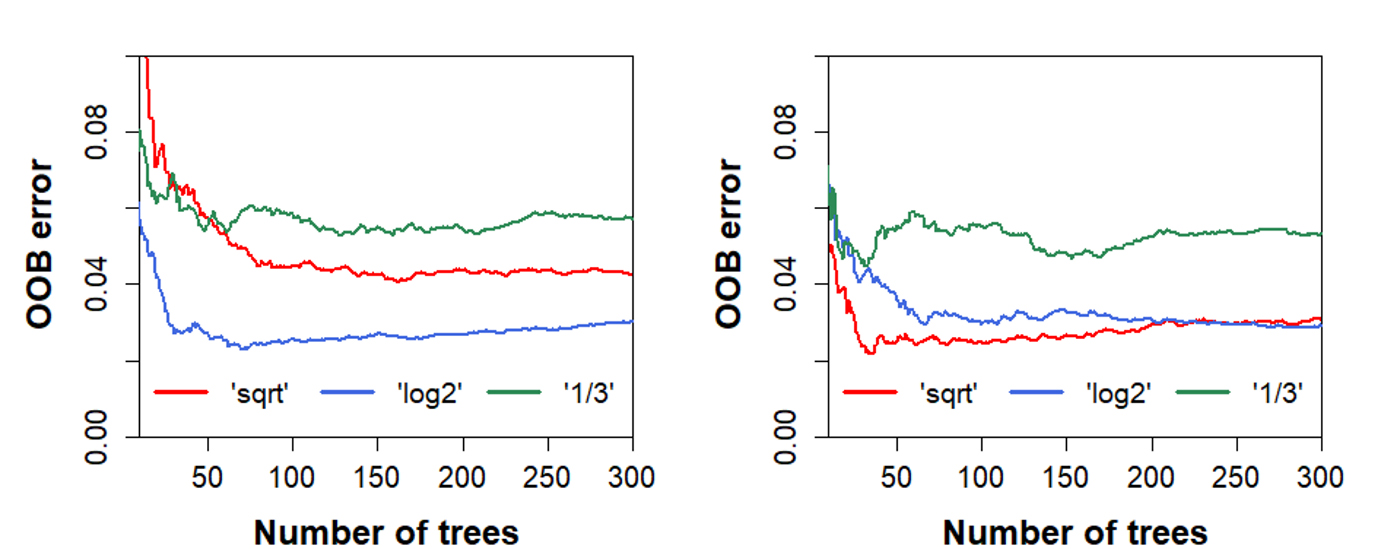
Fig. 5는 RF의 앙상블 학습 과정에서 의사결정에 참여하는 DT의 개수가 증가함에 따른 OOB 오류의 변화를 나타낸 것이다. DT의 개수가 증감함에 따라 OOB 오류는 점차 감소하였으며, DT의 수가 50개에 도달하였을 때를 기점으로 OOB 오류의 변화는 안정세를 나타내는 것으로 확인되었다. 원본 스펙트럼의 학습과정을 나타내는 Fig. 5a에서는 입력 변수의 개수를 입력변수 수량의 ‘log2’로, 2차 미분 스펙트럼(Fig. 5b)의 경우 입력변수 수량의 ‘sqrt’로 설정하는 것이 최소 OOB 오류 도달에 유리한 것으로 분석되었다. 또한 OOB 오류의 감소는 원본 스펙트럼으로 학습되었을 때에 비하여 2차 미분 스펙트럼으로 학습되었을 때 보다 빠르게 진행되었다. 이는 스펙트럼의 2차 미분과정을 통해 증폭된 아세틸화 유래 피크가 모델의 의사 결정 과정을 단순화하기 때문인 것으로 사료된다.17)
Table 2는 RF의 DS 예측 성능과 최적화 매개변수를 도시한 것이다. 학습 과정에 필요한 입력변수 수량을 나타내는 n_feature는 그 수가 클수록 모델 학습에 필요한 입력 변수의 수량이 증가하는 것을 의미하며 이는 모델의 과적합(overfitting) 가능성과 일반화 오류를 증가시킬 수 있다. 또한 랜덤포레스트의 학습과정에 참여하는 결정 나무의 개수를 의미하는 n_tree 역시 그 수치가 클수록 과적합의 가능성을 증가시키며, 일반화 성능이 저하된다. Table 2에서 확인할 수 있듯이 RF 모델링에 있어 스펙트럼의 2차 미분 전처리는 모델의 효용성을 증대함에 있어 유효한 것으로 나타났다.
Table 2.
Performance of random forest models for predicting degree of substitution in cellulose acetate
| Preprocessing | Hyperparameter | Train set | Test set | |||
| n_feature | n_tree | R2 | RMSE | R2 | RMSE | |
| Original | log2 | 75 | 0.993 | 0.078 | 0.986 | 0.100 |
| Second derivative | Sqrt | 37 | 0.996 | 0.066 | 0.988 | 0.090 |
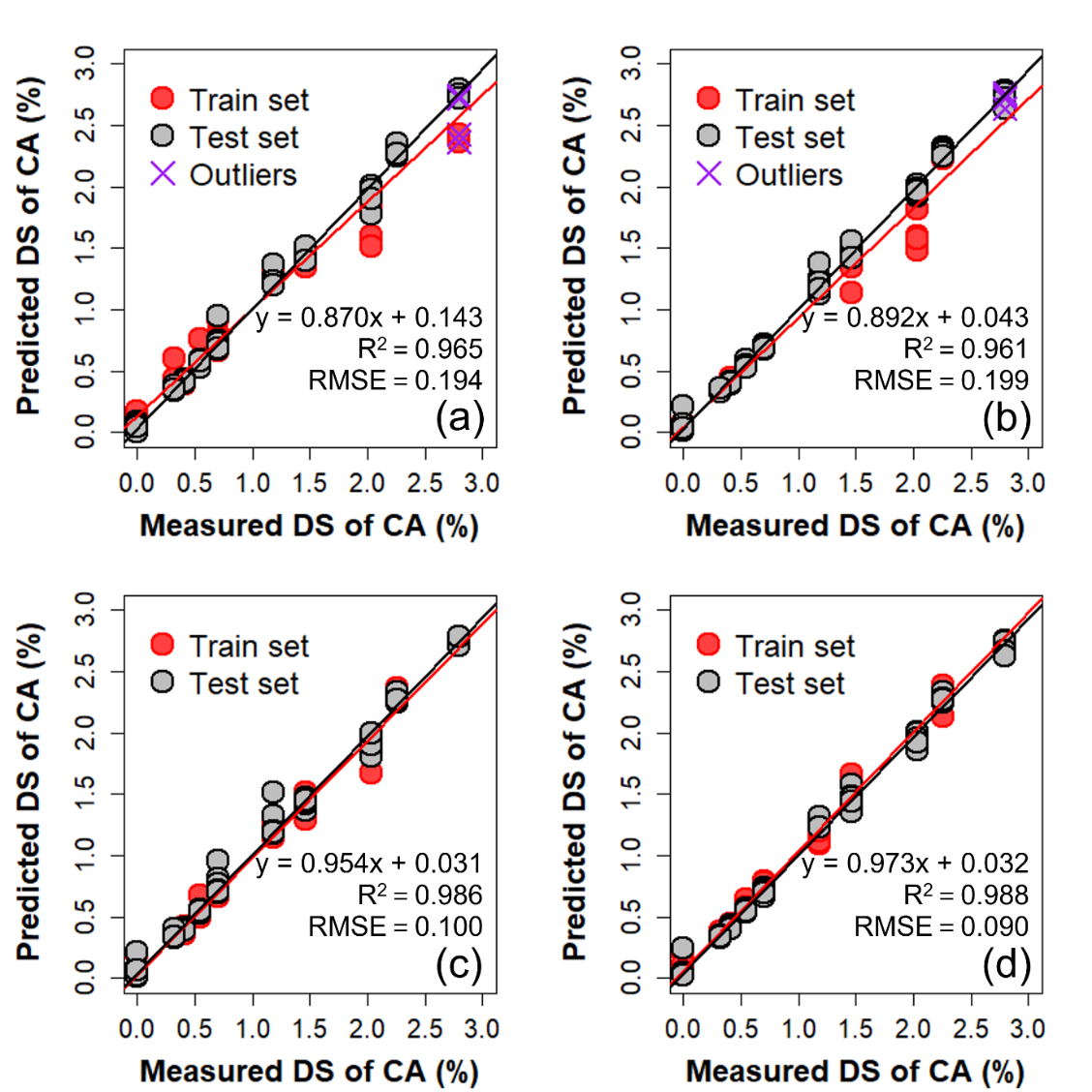
Fig. 6은 데이터 세트 내부에 이상치 포함 여부에 따른 RF 모델의 예측 성능을 나타낸 것이다. Fig. 6에 제시된 예측성능의 경우 모두 테스트 데이터 세트에 대한 예측성능을 도시하였다. Fig. 6a와 Fig. 6b는 각각 이상치를 포함한 데이터 세트에 대한 원본 IR 스펙트럼과 2차 미분 IR 스펙트럼을 통한 예측 수행결과를 나타낸다. 이상치가 포함된 데이터 세트에서는 스펙트럼 전처리 이후 결정계수가 0.965에서 0.961로 근소하게 감소하는 것으로 분석되었다. 그러나 Fig. 6c와 Fig. 6d의 이상치가 제거된 데이터 세트의 경우 Table 2에서 확인하였듯 스펙트럼 전처리에 따라 모델의 정확도가 개선되었다. 또한 이상치가 제거되지 않은 데이터세트를 이용하여 모델링을 진행할 때보다 예측 정확도가 상승하였다. 이는 DBSCAN 분석을 수행하여 이상치를 사전에 탐지하고 모델 학습에 앞서 IR 스펙트럼 데이터를 2차 미분하는 것이 모델 정확도 개선에 효과적임을 의미한다.18,29) 따라서 이하의 기계학습 모델링에는 모두 이상치가 제거된 2차 미분 스펙트럼 데이터 세트를 사용하였다.
3.4 셀룰로오스 아세테이트의 치환도 예측을 위한 스펙트럼 변수 중요도
3.4.1 변수 중요도
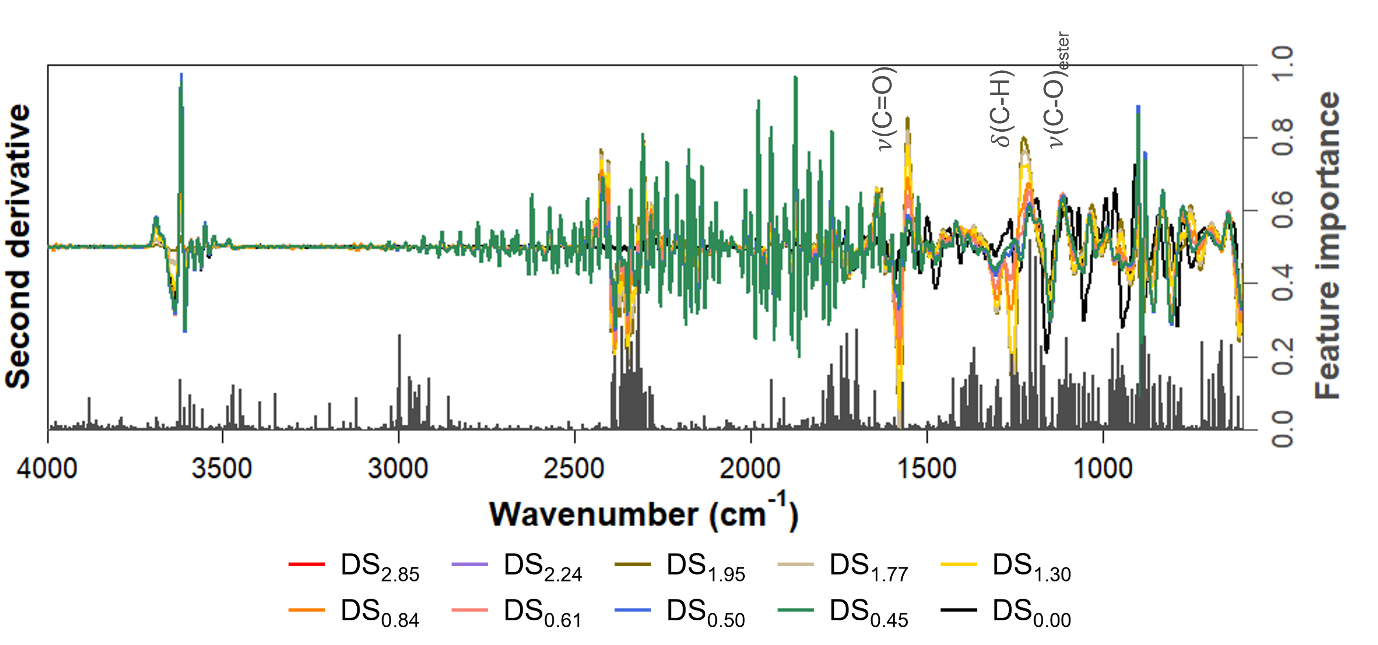
Fig. 7은 랜덤 포레스트 모델링 과정에서 각 입력 변수가 결정 나무의 노드 분할에 따른 불순도 감소에 기여하는 정도를 평가하여 산출된 변수 중요도를 나타낸다. 각 스펙트럼 영역에 해당하는 입력변수의 중요도가 클수록 모델의 의사결정에 기여한 정도가 높은 변수로 여겨진다. CA의 DS 예측을 위해 중요도가 높다고 여겨지는 IR 영역은 2450–2350 cm-1, 1800–1700 cm-1 및 1500–800 cm-1 흡수대인 것으로 분석되었다.
2700–1900 cm-1(zero-filled points) 흡수대의 경우 노이즈 피크 또는 셀룰로오스 재료의 특성화에 있어 유효하지 않은 정보를 포함한다.16,21) 특히 2450–2350 cm-1 흡수대의 중요도가 높게 측정된 것은 스펙트럼의 2차 미분 과정에서 노이즈 역시 함께 증폭됨에 따른 결과로 해석된다.33) 그 외 1800–1700 cm-1 및 1500–800 cm-1 흡수대의 경우 1750 cm-1, 1370 cm-1 및 1240 cm-1 흡수대와 같이 아세틸화 유래 피크를 포함하거나 cellulose finger print의 관련이 있는 영역으로 확인되었다. 즉, CA의 DS 예측 모델링에 있어 RF 모델이 주로 중요도가 높다고 판단하는 IR 영역은 아세틸화 유래 피크와 관련된 지역에 분포하고 있는 것으로 해석된다. 따라서 노이즈가 포함된 영역을 학습을 위한 입력 변수로부터 제거하면 모델의 성능을 향상시킬 수 있을 것으로 기대된다.16) 또한 학습 모델의 훈련과정에서 과도한 입력변수의 제공은 계산 비용의 증가를 유도하여 최종 모델의 과적합 위험성을 상승시키고 일반화 성능을 저하시킨다.34) 따라서 적절한 입력 변수의 설정을 통해 모델의 복잡도를 낮추어 학습 모델의 강건성(robustness)을 향상시키는 것이 예측 모델링의 궁극적 목표이다.16,17,21,29,34)
3.4.2 변수 중요도에 따른 변수 선택
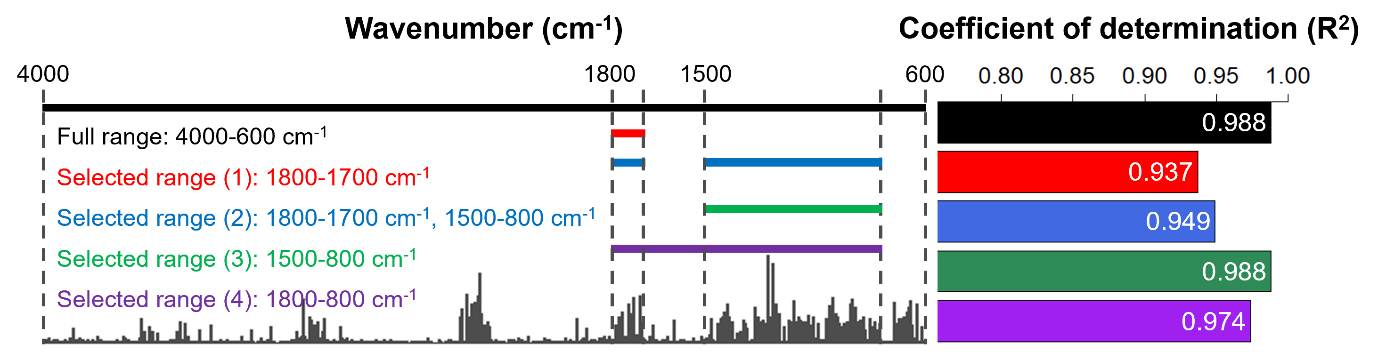
Fig. 8은 Fig. 7의 변수 중요도를 기반으로 설정한 선택 변수(selected variables)와 해당 선택 변수의 설정에 따른 모델의 예측 성능을 나타낸 것이다. 입력변수에 해당하는 스펙트럼 영역을 1800–1700 cm-1로 축소하였을 때 결정계수가 0.937로 전체 영역을 학습하였을 때 보다 약 5% 감소하였다. 이는 지나치게 줄어든 입력변수가 모델의 훈련을 위한 충분한 정보를 제공하지 못하였기 때문으로 판단된다.34) 한편 입력 변수에 해당하는 스펙트럼 영역을 1500–800 cm-1로 설정하였을 경우 결정계수는 0.988로 전체 스펙트럼 영역에 해당하는 변수를 사용하였을 때와 동일한 예측 성능을 나타냈다. 초기 설정한 전체 영역(full range)에 해당하는 입력변수의 개수는 7,049개, 축소된 1500–800 cm-1 영역의 입력변수는 1,453개로 구성되어 있었다. 즉, 입력변수의 79%에 해당하는 데이터를 축소하였는데도 불구하고 변수 축소 이전과 같은 예측성능을 나타낸 것이다. 이는 변수 선택을 통해 제거된 구간에 해당되는 스펙트럼 영역에서 모델의 의사결정에 필요하지 않은 노이즈와 중요도가 다소 낮은 구간의 데이터들이 제거됨에 따른 결과로 사료된다. 그러나 1800–1700 cm-1 영역과 1500–800 cm-1 영역을 동시에 적용했을 경우 결정계수가 0.949로 오히려 예측 성능이 저하되었다. 이는 1800–1700 cm-1 영역 내에서 아세틸기에 의하여 할당된 흡수대인 1750 cm-1(C=O stretching of the acetyl group)을 제외한 나머지 입력변수가 모델의 의사결정을 위한 유효 피크로 작용하지 않기 때문인 것으로 판단된다.11,12) 일반적으로 셀룰로오스 재료의 분석에 주로 사용되는 영역인 1800–800 cm-1 영역에서의 예측 성능 역시 상기와 같은 이유로 비교적 낮았던 것으로 사료된다.35) 이상의 결과를 종합하였을 때 적외선 분광분석을 통한 셀룰로오스 아세테이트의 치환도 예측 모델링에 있어 변수 중요도 기반의 변수 선택은 모델의 계산 비용 절감에 기여할 뿐만 아니라, 노이즈 및 스펙트럼 이동(shifts) 등 환경 변수에 따른 모델의 대응력을 향상시키는 데 효과적일 것으로 판단된다.16,34)
3.5 셀룰로오스 아세테이트의 치환도 예측을 위한 모델 성능 비교
Table 3은 셀룰로오스 아세테이트의 치환도 예측을 위해 생성된 RF와 예측 성능을 비교하기 위해 PLSR 및 MLP 모델을 활용하여 예측 모델링을 수행하고, 그 결과를 도시한 것이다. PLSR의 경우 전체 영역을 학습하였을 때 결정 계수는 0.969, 평균 제곱근 편차는 0.172를 기록하였다. Fig. 7과 Fig. 8의 결과로부터 설정한 축소 영역인 1500–800 cm-1 영역의 학습을 통한 예측 모델링 결과, 결정 계수는 0.966, 평균 제곱근 편차는 0.165로 전체 영역을 학습한 결과보다 다소 낮은 성능을 나타냈다. 또한 Table 2와 Fig. 6에 제시된 RF와 비교하였을 때 상대적으로 낮은 예측 성능을 나타냈다. 이는 독립변수와 종속변수 간의 공분산을 통해 선형 조합을 기반으로 추출되는 PLS factor가 비선형 관계를 탐색하는 RF에 비하여 변수 해석에 대한 능력이 상대적으로 낮기 때문으로 판단된다.16,34)
Table 3.
Comparison of performance for predicting degree of substitution in cellulose acetate
한편 MLP의 경우 1500–800 cm-1의 축소 영역의 적용 시 예측 성능의 향상을 유도할 수 있었으나 RF에 비하여 낮은 결정계수를 기록하였다. 이는 일반적으로 데이터 세트의 규모가 클 때 예측 성능이 우수하다고 알려진 MLP의 경우 100개의 IR 스펙트럼으로 구성된 본 데이터 세트의 구성이 이의 특성을 충족하지 못하였기 때문으로 판단된다.17) 또한 MLP의 모델링 과정에서 다양한 수량의 노드를 보유한 은닉층을 배치하여 최적 매개변수를 탐색하였으나 최종 선택된 모델의 경우 최소의 노드와 1개의 은닉층을 보유한 가장 단순한 모델의 예측 성능이 가장 높은 것으로 분석되었다. 이는 CA의 DS 예측 모델링을 위한 학습 데이터인 IR 스펙트럼의 구조가 비교적 복잡하지 않은 형태를 보유함에 따른 결과로 사료된다.33) 최종적으로, 변수 선택과 2차 미분을 통한 스펙트럼의 전처리는 모델 학습에 유용하지 않은 노이즈를 제거하고 1750 cm-1(C=O stretching of the acetyl group)와 같은 주요 피크를 강조함으로써 예측 모델의 정확도 향상에 기여할 수 있는 것으로 확인되었다. 또한 모델의 복잡도와 정확도를 고려하였을 때 RF 모델의 선택은 CA의 DS 예측 모델링을 위해 유용한 모델이라 판단된다.
그러나 본 연구에서 생성된 예측 모델의 경우 예측 대상이 되는 재료가 변화함에 따른 일반화 성능은 보장할 수 없으며 특정 모델에 대한 효용성을 완전히 대체할 수 없음을 유의해야 한다.
4. 결 론
본 연구에서는 랜덤포레스트 모델과 적외선 분광 분석을 결합하여 셀룰로오스 아세테이트의 치환도 예측 모델링과 변수 중요도를 분석하였다. 기계학습 모델의 구축에 앞서 DBSCAN을 통한 이상치 탐지와 IR 스펙트럼의 2차 미분 전처리는 예측 모델의 성능개선에 효과적인 것으로 확인되었다. 셀룰로오스 아세테이트의 치환도 예측 모델링을 위한 변수 중요도 분석결과 1500–800 cm-1 영역의 데이터가 상대적으로 높은 중요도를 갖는 변수로 분석되었다. 스펙트럼 영역의 선택적 적용(1500–800 cm-1)에 따른 랜덤포레스트의 예측성능은 결정계수 0.988로 기존 전체 영역에 대한 학습 결과와 동일하였다. 상기와 같은 과정을 통하여 계산 비용을 최소화하면서도 모델의 예측 정확도는 유지할 수 있는 셀룰로오스 아세테이트 치환도 예측 모델을 생성할 수 있었다. 상기 연구결과를 종합하였을 때 적외선 분광 분석과 기계 학습의 결합은 셀룰로오스 재료의 특성화를 위한 주요 분석도구로 활용될 수 있을 것이라 기대된다. 현재 셀룰로오스 아세테이트 외에도 카르복시메틸셀룰로오스(carboxymethyl cellulose, CMC), 메틸셀룰로오스(methyl cellulose), 아민화 셀룰로오스(aminated cellulose), 인산화 셀룰로오스(cellulose phosphate) 등 다양한 셀룰로오스 유도체의 특성화를 목표로 기계학습 기반 예측 모델을 개발하는 연구가 진행 중에 있으며, 해당 연구의 결과는 추후 보고될 예정이다.